Question

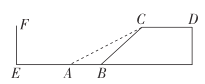
【题目】如图，已知正方形中，平分且交边于点，将绕点顺时针旋转到的位置，并延长交于点．

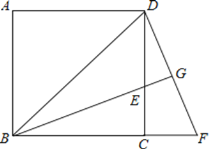
（1）求证：；

（2）若，求的长．

Answer 1

【答案】（1）见解析；（2）4

【解析】

（1）根据旋转的性质和角平分线的性质求出∠EDG=∠EBC=∠DBE，再结合公共角∠BGD＝∠DGE，根据相似三角形的判定定理即可证明；

（2）先根据相似三角形对应边成比例可求得DG=2，再证明△BDG≌△BFG，可得DF=4，

由此根据旋转的性质可求得BE=4．

（1）证明： ∵BE平分∠DBC，

∴∠CBE＝∠DBG，

∵将△BCE绕点C顺时针旋转到△DCF的位置，

∴∠CBE＝∠CDF，

∴∠DBG＝∠CDF，

∵∠BGD＝∠DGE，

∴△BDG∽△DEG．

（2）∵△BDG∽△DEG，

，

∴DG2＝BG·EG＝4，

∴DG＝2．

∵四边形ABCD是正方形，
∴∠DCB=90°，

∴∠EBC＋∠BEC＝90°，

∵∠BEC＝∠DEG，∠EBC＝∠EDG，

∴∠BGD＝90°，

∵∠DBG＝∠FBG，BG＝BG

∴△BDG≌△BFG，

∴FG＝DG＝2，

∴DF＝4，

∵将△BCE绕点C顺时针旋转到△DCF的位置，

∴BE＝DF＝4．