题目内容
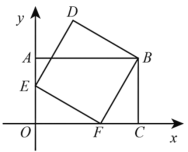
【题目】如图,在平面直角坐标系xOy中,点A、C、F在坐标轴上,E是OA的中点,四边形AOCB是矩形,四边形BDEF是正方形,若点C的坐标为(3,0), 则点D的坐标为( )
A. (1, 3)B. (1,![]() )C. (1,
)C. (1,![]() )D. (
)D. (![]() ,
,![]() )
)
【答案】A
【解析】
过D作DH⊥y轴于H,根据矩形和正方形的性质得到AO=BC,DE=EF=BF,∠AOC=∠DEF=∠BFE=∠BCF=90°,根据全等三角形的性质即可得到结论.
过D作DH⊥y轴于H,
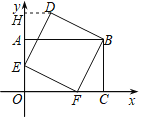
∵四边形AOCB是矩形,四边形BDEF是正方形,
∴AO=BC,DE=EF=BF,
∠AOC=∠DEF=∠BFE=∠BCF=90°,
∴∠OEF+∠EFO=∠BFC+∠EFO=90°,
∴∠OEF=∠BFO,
∴△EOF≌△FCB(ASA),
∴BC=OF,OE=CF,
∴AO=OF,
∵E是OA的中点,
∴OE=![]() OA=
OA=![]() OF=CF,
OF=CF,
∵点C的坐标为(3,0),
∴OC=3,
∴OF=OA=2,AE=OE=CF=1,
同理△DHE≌△EOF(ASA),
∴DH=OE=1,HE=OF=2,
∴OH=2,
∴点D的坐标为(1,3),
故选A.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目