题目内容
【题目】某乡镇实施产业扶贫,帮助贫困户承包了荒山种植蜜柚,已知该蜜柚的成本价为8元/千克。
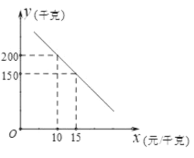
到了收获季节,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销量
干克)与销售单价x(元/千克)之间的函数关系如图所示.
(1)求y与x的函数关系式,并写出x的取值范围:
(2)当该蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
(3)某农户今年共采摘蜜柚4800千克,该蜜柚的保持期为40天,根据(2)中获得最大利润的方式进行销售,能否销售完这批蜜柚?请说明理由.
【答案】(1)y与x的函数关系式为y=-10x+300(8≤x≤30);(2)x=19时,w取得最大值,最大值为1210;(3)不能销售完这批蜜柚.
【解析】
(1)利用待定系数法求解可得;
(2)根据“总利润=单件利润×销售量”列出函数解析式,并配方成顶点式即可得出最大值;
(3)求出在(2)中情况下,即x=19时的销售量,据此求得40天的总销售量,比较即可得出答案.
(1)设y与x的函数关系式为y=kx+b,
将(10,200)、(15,150)代入,得:![]() ,
,
解得:![]() ,
,
∴y与x的函数关系式为y=-10x+300(8≤x≤30);
(2)设每天销售获得的利润为w,
则w=(x-8)y
=(x-8)(-10x+300)
=-10(x-19)2+1210,
∵8≤x≤30,
∴当x=19时,w取得最大值,最大值为1210;
(3)由(2)知,当获得最大利润时,定价为19元/千克,
则每天的销售量为y=-10×19+300=110千克,
∵保质期为40天,
∴总销售量为40×110=4400,
又∵4400<4800,
∴不能销售完这批蜜柚.

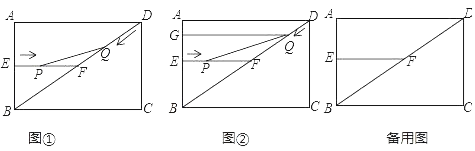
【题目】如图1是边长为![]() 的正方形薄铁片,小明将其四角各剪去一个相同的小正方形(图中阴影部分)后,发现剩余的部分能折成一个无盖的长方体盒子,图2为盒子的示意图(铁片的厚度忽略不计).
的正方形薄铁片,小明将其四角各剪去一个相同的小正方形(图中阴影部分)后,发现剩余的部分能折成一个无盖的长方体盒子,图2为盒子的示意图(铁片的厚度忽略不计).
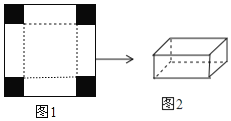
(1)设剪去的小正方形的边长为![]() ,折成的长方体盒子的容积为
,折成的长方体盒子的容积为![]() , 用只含字母
, 用只含字母![]() 的式子表示这个盒子的高为________
的式子表示这个盒子的高为________![]() ,底面积为________
,底面积为________![]() ,盒子的容积
,盒子的容积![]() 为________
为________![]() ;
;
(2)为探究盒子的体积与剪去的小正方形的边长![]() 之间的关系,小明列表
之间的关系,小明列表
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|
| _______ |
|
|
| _______ |
|
|
请将表中数据补充完整,并根据表格中的数据写出当![]() 的值逐渐增大时,
的值逐渐增大时,![]() 的值如何变化?
的值如何变化?
【题目】下表是小明记录的今年雨季一周河水的水位变化情况(上周末的水位达到警戒水位).
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位变化/米 | +0.20 | +0.81 | ﹣0.35 | +0.03 | +0.28 | ﹣0.36 | ﹣0.01 |
注:正号表示水位比前一天上升,负号表示水位比前一天下降.
(1)本周哪一天河流的水位最高?哪一天河流的水位最低?它们位于警戒水位之上还是之下?与警戒水位的距离分别是多少米?
(2)与上周相比,本周末河流水位是上升了还是下降了?