Question

【题目】如图，点D是△ABC内一点，点E，F，G，H分别是AB，AC，CD，BD的中点。

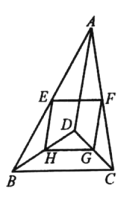
（1）求证：四边形EFGH是平行四边形；（2）已知AD＝6，BD＝4，CD＝3，∠BDC＝90°，求四边形EFGH的周长。

Answer 1

【答案】（1）见解析；（2）周长为：11.

【解析】

（1）根据三角形的中位线的定理和平行四边形的判定即可解答；

（2）利用勾股定理列式求出BC的长，再根据三角形的中位线平行于第三边并且等于第三边的一半求出EH=FG=AD，EF=GH=BC，然后代入数据进行计算即可得解.

（1）证明：∵点E，F 分别是AB，AC 的中点，

∴EF 是△ABC 的中位线，∴EF∥BC 且EF＝BC；

又∵点H，G 分别是BD，CD 的中点，∴HG 是△BCD 的中位线，∴HG∥BC

且HG＝BC；

∴EF∥HG 且EF＝HG，∴四边形EFGH 是平行四边形.

（2）∵点E，H 分别是AB，BD 的中点，∴EH 是△ABD 的中位线，∴EH＝AD＝3；

∵∠BDC＝90°，∴△BCD 是直角三角形；

在Rt△BCD 中，CD＝3，BD＝4，∴由勾股定理得：BC＝5；

∵HG＝BC，∴HG＝；

由（1）知，四边形EFGH 是平行四边形，∴周长为2EH+2HG＝11.