题目内容
如图,点A为x轴负半轴上一点,点B为x轴正半轴上一点,OA,OB(OA?OB)的长分别是关于x的一元二次方程x2-4mx+m2+2=0的两根,C(0,3),且△ABC的面积为6,
(1)求∠ABC的度数;
(2)如图二,过点C作CD⊥AC交x轴于点D,求点D的坐标.
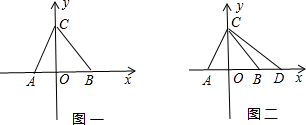
(1)求∠ABC的度数;
(2)如图二,过点C作CD⊥AC交x轴于点D,求点D的坐标.
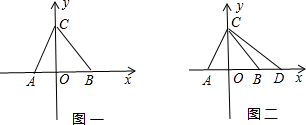
(1)∵C(0,3)
∴OC=3,
∵△ABC的面积为6,
∴AB=4,
∵OA、OB的长分别是关于x的一元二次方程x2-4mx+m2+2=0的两根,
∴OA+OB=4m=4
∴m=1
∴一元二次方程x2-4mx+m2+2=0可化为:x2-4x+3=0
解得:x1=1 x2=3
即OA=1,OB=3
在Rt△OBC中,OB=OC
∴∠ABC=45°;
(2)设D点坐标为(x,0)
在Rt△ACD中
AC2+CD2=AD2
即:(1-0)2+(0-3)2+(x-0)2+(0-3)2=(1+x)2
解得:x=9
即:D点坐标为(9,0).
∴OC=3,
∵△ABC的面积为6,
∴AB=4,
∵OA、OB的长分别是关于x的一元二次方程x2-4mx+m2+2=0的两根,
∴OA+OB=4m=4
∴m=1
∴一元二次方程x2-4mx+m2+2=0可化为:x2-4x+3=0
解得:x1=1 x2=3
即OA=1,OB=3
在Rt△OBC中,OB=OC
∴∠ABC=45°;
(2)设D点坐标为(x,0)
在Rt△ACD中
AC2+CD2=AD2
即:(1-0)2+(0-3)2+(x-0)2+(0-3)2=(1+x)2
解得:x=9
即:D点坐标为(9,0).

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目

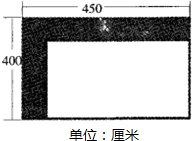 下,小明家至少需要多少块地砖?
下,小明家至少需要多少块地砖?