题目内容
【题目】如图,在直角梯形ABCD中,AD∥BC , ∠ABC= ![]() ,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )
,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( ) 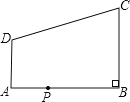
A.1个
B.2个
C.3个
D.4个
【答案】C
【解析】解答:∵AB⊥BC , ∴∠B= ![]() .
.
∵AD∥BC ,
∴∠A=180°-∠B= ![]() ,
,
∴∠PAD=∠PBC= ![]() .AB=8,AD=3,BC=4,
.AB=8,AD=3,BC=4,
设AP的长为x , 则BP长为8-x .
若AB边上存在P点,使△PAD与△PBC相似,那么分两种情况:
①若△APD∽△BPC , 则AP:BP=AD:BC , 即x:(8-x)=3:4,解得x= ![]() ;
;
②若△APD∽△BCP , 则AP:BC=AD:BP , 即x:4=3:(8-x),解得x=2或x=6.
∴满足条件的点P的个数是3个,
故选:C.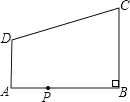
分析:因为∠PAD=∠PBC= ![]() ,所以要使△PAD与△PBC相似,分两种情况讨论:①△APD∽△BPC , ②△APD∽△BCP , 这两种情况都可以根据相似三角形对应边的比相等求出AP的长,从而得到P点的个数.进行分类讨论是解答此题的关键.
,所以要使△PAD与△PBC相似,分两种情况讨论:①△APD∽△BPC , ②△APD∽△BCP , 这两种情况都可以根据相似三角形对应边的比相等求出AP的长,从而得到P点的个数.进行分类讨论是解答此题的关键.
【考点精析】解答此题的关键在于理解相似三角形的判定的相关知识,掌握相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS).

练习册系列答案
相关题目