Question

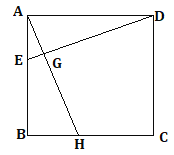
【题目】如图，点E、H分别在正方形ABCD的边AB、BC上，且AE=BH

求证：（1）DE=AH （2）DE⊥AH

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】（1）根据正方形的性质可得AD=AB， ∠DAE=∠ABC，然后利用“边角边”证明△AD和△BHA全等，根据全等三角形对应边相等可得DE=AH；

（2）根据全等三角形对应角相等可得∴∠EDA=∠HAB，然后求出∠EDA+∠HAD =∠DAE=90°，判断出AH⊥DE．

(1)∵四边形ABCD是正方形，

∴AD=AB， ∠DAE=∠ABC，

∵AE=BH

∴△AED≌△BHA（SAS）

∴DE=AH

(2) ∵△AED≌△BHA

∴∠EDA=∠HAB

∵∠HAB+∠HAD=90°

∴∠EDA+∠HAD=90°

∴DE⊥AH