题目内容
【题目】如图，把矩形ABCD对折，折痕为MN ， 矩形DMNC与矩形ABCD相似，已知AB=4．
（1）求AD的长；
（2）求矩形DMNC与矩形ABCD的相似比．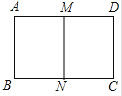
【答案】
（1）
解答：由已知得MN=AB，MD= 
AD= BC，
∵矩形DMNC与矩形ABCD相似，
∴ 
，
∵MN=AB，DM= AD，BC=AD，
∴ 
，
∴由AB=4得，AD= 
；
（2）
矩形DMNC与矩形ABCD的相似比为 
．
【解析】 矩形DMNC与矩形ABCD相似，对应边的比相等，可以求出AD的长；相似比就是对应边的比．此题考查相似多边形的性质，对应边的比相等．
【考点精析】掌握翻折变换（折叠问题）是解答本题的根本，需要知道折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．
练习册系列答案
名校课堂系列答案
相关题目
