题目内容
若二次函数y=ax2+bx+c的x与y的部分对应值如下表:
①抛物线与x轴的一个交点为(3,0); ②函数y=ax2+bx+c的最大值为6;
③抛物线的对称轴是直线x=
; ④在对称轴左侧,y随x增大而增大.
从上表可知,以上说法中正确的是
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
③抛物线的对称轴是直线x=
| 1 |
| 2 |
从上表可知,以上说法中正确的是
①③④
①③④
.(填写序号)分析:根据表中数据可知,当x=0时,y=6;当x=1时,y=6,由抛物线的对称性,可得到对称轴是直线x=
;又当x=-2时,y=0,所以抛物线与x轴的另外一个交点为(3,0);而抛物线的开口向下,因此可得在对称轴左侧,y随x增大而增大.
| 1 |
| 2 |
解答:解:根据图表,当x=0时,y=6;当x=1时,y=6,由抛物线的对称性,可得到对称轴是直线x=
,故③正确;
当x=-2,y=0,根据抛物线的对称性,当x=3时,y=0,即抛物线与x轴的交点为(-2,0)和(3,0),故①正确;
根据表中数据得到抛物线的开口向下,所以当x=
时,函数有最大值,而不是x=0,或1对应的函数值6,故②错误;
并且在直线x=
的左侧,y随x增大而增大,故④正确.
所以①③④正确,②错误.
故答案①③④.
| 1 |
| 2 |
当x=-2,y=0,根据抛物线的对称性,当x=3时,y=0,即抛物线与x轴的交点为(-2,0)和(3,0),故①正确;
根据表中数据得到抛物线的开口向下,所以当x=
| 1 |
| 2 |
并且在直线x=
| 1 |
| 2 |
所以①③④正确,②错误.
故答案①③④.
点评:本题考查了抛物线y=ax2+bx+c的性质:抛物线是轴对称图形,它与x轴的两个交点是对称点,对称轴与抛物线的交点为抛物线的顶点;a<0时,函数有最大值,在对称轴左侧,y随x增大而增大.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
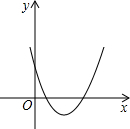 (1998•大连)若二次函数y=ax2+bx+c(a≠0)的图象如图,则直线y=bx-c不经过( )
(1998•大连)若二次函数y=ax2+bx+c(a≠0)的图象如图,则直线y=bx-c不经过( )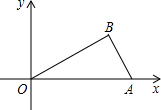 如图,已知点O为坐标原点,∠AOB=30°,∠B=90°,且点A的坐标为(2,0).
如图,已知点O为坐标原点,∠AOB=30°,∠B=90°,且点A的坐标为(2,0).