题目内容
【题目】如图所示,已知O是直线AB上一点,∠BOE=∠FOD=90°,OB平分∠COD
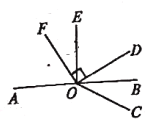
(1)图中与∠DOE互余的角是______________________
(2)图中是否有与∠DOE互补的角?如果有,直接写出全部结果;如果没有,说明理由。
(3)如果∠EOD︰∠EOF=3︰2,求∠AOC的度数
【答案】(1)∠EOF、∠BOD、∠BOC;(2)有,∠BOF和∠EOC;(3)144°
【解析】
(1)由∠BOE=90°,则∠DOE+∠BOD=90°,要求与∠DOE互余的角,只要找到与∠BOD相等的角即可,即∠BOC,∠EOF;
(2)根据同角的余角相等,结合OB平分∠COD,可得∠DOE=∠AOF,∠EOF=∠BOD=∠BOC,则∠DOE的补角与∠AOF的补角相等,即∠DOE互补的角:∠BOF、∠EOC;
(3)由∠EOD︰∠EOF=3︰2,则求出∠EOF=36°,即可得到∠BOC=36°,利用互补关系,即可得到∠AOC的度数.
解:(1)∵∠BOE=∠FOD=90°,
∴∠AOF+∠EOF=90°,∠BOD+∠DOE=90°,∠DOE+∠EOF=90°,
∵OB平分∠COD,
∴∠BOD=∠BOC,∠AOF=∠DOE,
∴与∠DOE互余的是:∠EOF、∠BOD、∠BOC;
故答案为:∠EOF、∠BOD、∠BOC;
(2)由(1)以及同角的余角相等可知,∠AOF=∠DOE,∠EOF=∠BOD=∠BOC,
∴∠DOE的补角与∠AOF的补角相等,
∵∠AOF+∠BOF=180°,∠BOF=∠EOC,
∴∠AOF+∠EOC=180°,
∴∠DOE的补角有:∠BOF和∠EOC;
(3)∵∠EOD︰∠EOF=3︰2,∠DOF=∠EOD+∠EOF=90°,
∴∠EOF=![]() ,
,
∴∠BOC=36°,
∴∠AOC=![]() .
.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案