ĖâÄŋÄÚČÝ
ĄūĖâÄŋĄŋÎŌĘÐÂĖŧŊēŋÃÅūöķĻĀûÓÃÏÖÓÐĩÄēŧÍŽÖÖĀāŧĻŧÜīîÅäÔ°ŌÕÔėÐÍĢŽ°Ú·ÅÓÚģĮĮøÖũŌŠīóĩĀĩÄÁ―ēāĢŪAĄĒBÁ―ÖÖÔ°ŌÕÔėÐÍūųÐčÓÃĩ―ķÅūéŧĻĢŽAÖÖÔėÐÍÃŋļöÐčÓÃķÅūéŧĻ25ÅčĢŽBÖÖÔėÐÍÃŋļöÐčÓÃķÅūéŧĻ35ÅčĢŽ―âīðÏÂÁÐÎĘĖâĢš
ĢĻ1ĢĐŌŅÖŠČËÃņīóĩĀÁ―ēāīîÅäĩÄAĄĒBÁ―ÖÖÔ°ŌÕÔėÐÍđē60ļöĢŽĮĄšÃÓÃÁË1700ÅčķÅūéŧĻĢŽAĄĒBÁ―ÖÖÔ°ŌÕÔėÐÍļũīîÅäÁËķāÉŲļöĢŋ
ĢĻ2ĢĐČįđûīîÅäŌŧļöAÖÖÔėÐÍĩÄģÉąūWÓëÔėÐÍļöĘý![]() ĩÄđØÏĩĘ―ÎŠĢšWĢ―100ĻD
ĩÄđØÏĩĘ―ÎŠĢšWĢ―100ĻD![]() x ĢĻ0ĢžxĢž50ĢĐĢŽīîÅäŌŧļöBÖÖÔėÐÍĩÄģÉąūΊ80ÔŠĢŪÏÖÔÚđÛšĢīóĩĀÁ―ēāŌēÐčīîÅäAĄĒBÁ―ÖÖÔ°ŌÕÔėÐÍđē50ļöĢŽŌŠĮóÃŋÖÖÔ°ŌÕÔėÐÍēŧĩÃÉŲÓÚ20ļöĢŽēĒĮŌģÉąūŨÜķîyĢĻÔŠĢĐŋØÖÆÔÚ4500ÔŠŌÔÄÚ. ŌÔÉÏŌŠĮóÄÜ·ņÍŽĘąÂúŨãĢŋĮëÄãÍĻđýžÆËãËĩÃũĀíÓÉ.
x ĢĻ0ĢžxĢž50ĢĐĢŽīîÅäŌŧļöBÖÖÔėÐÍĩÄģÉąūΊ80ÔŠĢŪÏÖÔÚđÛšĢīóĩĀÁ―ēāŌēÐčīîÅäAĄĒBÁ―ÖÖÔ°ŌÕÔėÐÍđē50ļöĢŽŌŠĮóÃŋÖÖÔ°ŌÕÔėÐÍēŧĩÃÉŲÓÚ20ļöĢŽēĒĮŌģÉąūŨÜķîyĢĻÔŠĢĐŋØÖÆÔÚ4500ÔŠŌÔÄÚ. ŌÔÉÏŌŠĮóÄÜ·ņÍŽĘąÂúŨãĢŋĮëÄãÍĻđýžÆËãËĩÃũĀíÓÉ.
Ąūīð°ļĄŋ(1) AÖÖÔ°ŌÕÔėÐÍīîÅäÁË40ļöĢŽBÖÖÔ°ŌÕÔėÐÍīîÅäÁË20ļö;(2) ĩą![]() ĘąĢŽĩÄŨîīóÖĩΊ
ĘąĢŽĩÄŨîīóÖĩΊ![]() ,4500ĢŽËųŌÔÄÜÍŽĘąÂúŨãĖâÉčŌŠĮó.
,4500ĢŽËųŌÔÄÜÍŽĘąÂúŨãĖâÉčŌŠĮó.
Ąū―âÎöĄŋ·ÖÎöĢš(1)ĄĒÉčAÖÖÔ°ŌÕÔėÐÍīîÅäÁËxļöĢŽÔōBÖÖÔ°ŌÕÔėÐÍīîÅäÁËĢĻ60ĐxĢĐļöĢŽļųūÝĖâŌâÁÐģö·―ģĖīÓķøĩÃģöxĩÄÖĩĢŧ(2)ĄĒÉčAÖÖÔ°ŌÕÔėÐÍīîÅäÁËxļöĢŽÔōBÖÖÔ°ŌÕÔėÐÍīîÅäÁËĢĻ50ĐxĢĐļöĢŽļųūÝĖâŌâĩÃģöyÓëxĩÄšŊĘýđØÏĩĘ―ĢŽĩÃģöŨîīóÖĩĢŽīÓķøŋÉŌÔÅÐķÏĘĮ·ņÕýČ·ĢŪ
Ïę―âĢšĢĻ1ĢĐÉčAÖÖÔ°ŌÕÔėÐÍīîÅäÁËxļöĢŽÔōBÖÖÔ°ŌÕÔėÐÍīîÅäÁËĢĻ60ĐxĢĐļöĢŽ
25x+35ĢĻ60ĐxĢĐ=1700ĢŽ ―âĩÃĢŽx=40ĢŽ60Đx=20ĢŽ
īðĢšAÖÖÔ°ŌÕÔėÐÍīîÅäÁË40ļöĢŽBÖÖÔ°ŌÕÔėÐÍīîÅäÁË20ļöĢŧ
ĢĻ2ĢĐÄÜÍŽĘąÂúŨãĖâÉčŌŠĮóĢŽ
ĀíÓÉĢšÉčAÖÖÔ°ŌÕÔėÐÍīîÅäÁËxļöĢŽÔōBÖÖÔ°ŌÕÔėÐÍīîÅäÁËĢĻ50ĐxĢĐļöĢŽ
ģÉąūŨÜķîyÓëAÖÖÔ°ŌÕÔėÐÍļöĘýÏëxĩÄšŊĘýđØÏĩĘ―ÎŠĢšy=xĢĻ100Đ![]() ĢĐ+80ĢĻ50ĐxĢĐ=Đ
ĢĐ+80ĢĻ50ĐxĢĐ=Đ![]() +20x+4000=
+20x+4000=![]() ĢŽ
ĢŽ
ĄßxĄÝ20ĢŽ50ĐxĄÝ20ĢŽ Ąā20ĄÜxĄÜ30ĢŽ Ąāĩąx=20ĘąĢŽyČĄĩÃŨîīóÖĩĢŽīËĘąy=4200ĢŽ
Ąß4200Ģž4500ĢŽ ĄāÄÜÍŽĘąÂúŨãĖâÉčŌŠĮóĢŪ

 ĩžŅ§ČŦģĖÁ·īīÓÅŅĩÁ·ÏĩÁÐīð°ļ
ĩžŅ§ČŦģĖÁ·īīÓÅŅĩÁ·ÏĩÁÐīð°ļĄūĖâÄŋĄŋČįÍžĒŲĢŽÔÚÕý·―ÐÎABCDÖÐĢŽ![]() ĢŽĩãEĢŽF·ÖąðÔÚBCĄĒCDÉÏĢŽ
ĢŽĩãEĢŽF·ÖąðÔÚBCĄĒCDÉÏĢŽ![]() ĢŽĘÔĖ―ūŋ
ĢŽĘÔĖ―ūŋ![]() ÃæŧýĩÄŨîÐĄÖĩĄĢ
ÃæŧýĩÄŨîÐĄÖĩĄĢ
ÏÂÃæĘĮÐĄĀöĩÄĖ―ūŋđýģĖĢš
(1)ŅÓģĪEBÖÁGĢŽĘđ![]() ĢŽÁŽ―ÓAGĢŽŋÉŌÔÖĪÃũ
ĢŽÁŽ―ÓAGĢŽŋÉŌÔÖĪÃũ![]() ĢŪĮëÍęģÉËýĩÄÖĪÃũĢŧ
ĢŪĮëÍęģÉËýĩÄÖĪÃũĢŧ
(2)Éč![]() ĢŽ
ĢŽ![]() ,
,![]()
ĒŲ―ášÏĢĻ1ĢĐÖÐ―áÂÛĢŽÍĻđýžÆËãĩÃĩ―![]() ÓëxĩÄēŋ·ÖķÔÓĶÖĩĄĢĮëĮóģöąíļņÖÐaĩÄÖĩĢšĢĻÐīģö―âīðđýģĖĢĐ
ÓëxĩÄēŋ·ÖķÔÓĶÖĩĄĢĮëĮóģöąíļņÖÐaĩÄÖĩĢšĢĻÐīģö―âīðđýģĖĢĐ
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 10 | 8.18 | 6.67 | 5.38 | 4.29 | 3.33 | a | 1.76 | 1.11 | 0.53 | 0 |
ĒÚĀûÓÃÉÏąíšÍĢĻ1ĢĐÖÐĩÄ―áÂÛÍĻđýÃčĩãĄĒÁŽÏßŋÉŌÔ·ÖąðŧģöšŊĘý![]() ĄĒ
ĄĒ![]() ĩÄÍžÏņĄĒĮëÔÚÍžĒÚÖÐÍęÉÆËýĩÄŧÍžĢŧ
ĩÄÍžÏņĄĒĮëÔÚÍžĒÚÖÐÍęÉÆËýĩÄŧÍžĢŧ
ĒÛļųūÝŌÔÉÏĖ―ūŋĢŽđĀžÆ![]() ÃæŧýĩÄŨîÐĄÖĩԞΊĢĻ―áđûđĀžÆĩ―0ĢŪ1ĢĐĄĢ
ÃæŧýĩÄŨîÐĄÖĩԞΊĢĻ―áđûđĀžÆĩ―0ĢŪ1ĢĐĄĢ
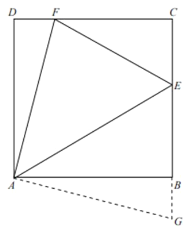
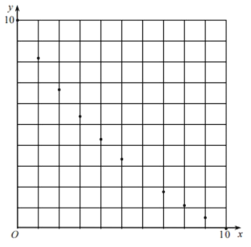
ÍžĒŲ ÍžĒÚ
ĄūĖâÄŋĄŋÎÂķČÍĻģĢÓÐÁ―ÖÖąíĘū·―·ĻĢšŧŠĘÏķČĢĻĩĨÎŧĢšĻHĢĐÓëÉãĘÏķČĢĻĩĨÎŧĢšĄæĢĐĢŽŌŅÖŠŧŠĘÏķČĘý![]() ÓëÉãĘÏķČĘý
ÓëÉãĘÏķČĘý![]() ÖŪžäĘĮŌŧīΚŊĘýđØÏĩĢŽÏÂąíÁÐģöÁËēŋ·ÖŧŠĘÏķČÓëÉãĘÏķČÖŪžäĩÄķÔÓĶđØÏĩĢš
ÖŪžäĘĮŌŧīΚŊĘýđØÏĩĢŽÏÂąíÁÐģöÁËēŋ·ÖŧŠĘÏķČÓëÉãĘÏķČÖŪžäĩÄķÔÓĶđØÏĩĢš
ÉãĘÏķČĘý | Ą | 0 | Ą | 35 | Ą | 100 | Ą |
ŧŠĘÏķČĘý | Ą | 32 | Ą | 95 | Ą | 212 | Ą |
ĢĻ1ĢĐŅĄÓÃąíļņÖÐļøģöĩÄĘýūÝĢŽĮóyđØÓÚxĩÄšŊĘý―âÎöĘ―Ģŧ
ĢĻ2ĢĐÓÐŌŧÖÖÎÂķČžÆÉÏÓÐÁ―ļöŋĖķČĢŽžīēâÁŋÄģŌŧÎÂķČĘąŨóąßĘĮÉãĘÏķČĢŽÓŌąßĘĮŧŠĘÏķČĢŽÄĮÃīÔÚķāÉŲÉãĘÏķČĘąĢŽÎÂķČžÆÉÏÓŌąßŧŠĘÏķČĩÄŋĖķČÕýšÃąČŨóąßÉãĘÏķČĩÄŋĖķČīó56Ģŋ