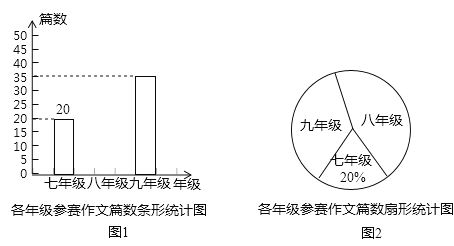
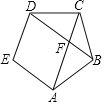
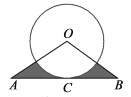
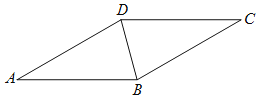
题目内容
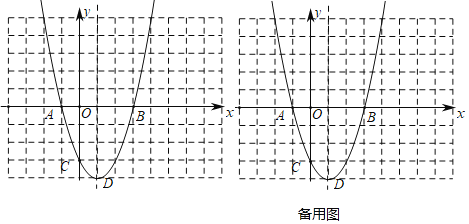
【题目】抛物线y=x2+bx+c与x轴分别交于点A．B，与y轴交于点C，A点坐标为（-1，0），B点坐标为（3，0），顶点为D．
（1）求抛物线解析式；
（2）若点M在抛物线的对称轴上，求△ACM周长的最小值；
（3）以点P为圆心的圆经过A、B两点，且与直线CD相切，求点P的坐标．
【答案】（1）y=x2-2x-3；（2）△ACM周长的最小值为3
+
；（3）点P的坐标为（1，4+2
）或（1，4-2）．
【解析】
（1）根据点A，B的坐标，利用待定系数法即可求出抛物线解析式；
（2）连接BC，交抛物线对称轴于点M，此时AM+CM取得最小值，最小值为BC的长度，利用二次函数图象上点的坐标特征可求出点C的坐标，根据点B，C的坐标，利用待定系数法即可求出直线BC的解析式，代入x=1即可求出点M的坐标，利用两点间的距离公式可求出BC，AC的长度，进而可得出△ACM周长的最小值；
（3）过点P作PE⊥CD，垂足为点E，则△PDE为等腰直角三角形，进而可得出PE=
PD，设点P的坐标为（1，m），由PA=PE可得出关于m的方程，解之即可得出点P的坐标．
（1）将A（-1，0），B（3，0）代入y=x2+bx+c，得：
，解得：
，
∴抛物线解析式为y=x2-2x-3．
（2）连接BC，交抛物线对称轴于点M，此时AM+CM取得最小值，最小值为BC的长度，如图1所示，
当x=0时，y=x2-2x-3=-3，
∴点C的坐标为（0，-3）．
设直线BC的解析式为y=kx+a（k≠0），
将B（3，0），C（0，-3）代入y=kx+a，得：
，解得：
，
∴直线BC的解析式为y=x-3．
∵y=x2-2x-3=（x-1）2-4，
∴抛物线的对称轴为直线x=1，顶点D的坐标为（1，-4）．
当x=1时，y=x-3=-2，
∴当点M的坐标为（1，-2）时，AM+CM取得最小值，最小值BC=
=3．
∵点A的坐标为（-1，0），点C的坐标为（0，-3），
∴AC=
=，
∴△ACM周长的最小值为3+．
（3）过点P作PE⊥CD，垂足为点E，如图2所示．
∵以点P为圆心的圆经过A、B两点，
∴点P在直线x=1上．
∵点C的坐标为（0，-3），点D的坐标为（1，-4），
∴直线CD的解析式为y=-x-3，
∴∠PDE=45°，
∴△PDE为等腰直角三角形，
∴PE=PD．
设点P的坐标为（1，m）．
∵PA=PE，
∴
=（m+4），
整理，得：m2-8m-8=0，
解得：m1=4+2，m2=4-2，
∴点P的坐标为（1，4+2）或（1，4-2）．
