Question

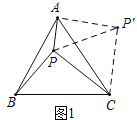
【题目】如图，⊙O的半径是2，弦AB=，点C为是优弧AB上一个动点，BD⊥BC交直线AC于点D，则△ABD的面积的最大值为___________ .

Answer 1

【答案】3

【解析】

连结OA，如图，∠AOB=120°，根据圆周角定理得∠ACB=∠AOB=60°，由于BC⊥BD，所以∠D=30°，因为AB=，则要使△ABD的最大面积，点D到AB的距离要最大；当点D在⊙M上的优弧AB的中点时，点D到AB的距离最大，从而得到△ABD的最大面积．

解：连结OA，过点O作OE垂直AB，交AB与点E

已知⊙O的半径是2，弦AB=，BE⊥BC，根据垂径定理和勾股定理可得

OE=1，AE=，sin∠OAE=

∴∠OAE=∠OBE=30°

（同弧所对的圆周角是圆心角的一半）

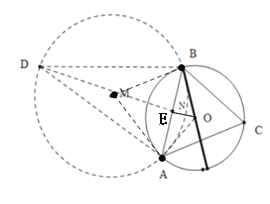
∠ADB =30°，点D在以AB为弦的⊙M上运动，

∠BMA=60°，

AB=MB=DM=MA=，

当点D在优弧AB的中点时，点D到AB的距离最大，从而得到△ABD的最大面积．

过点D作DN⊥AB于点N

故答案为.