Question

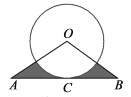
【题目】如图，已知直线AB经过⊙O上的点C，且OA=OB，CA=CB.

(1)求证：直线AB是⊙O的切线；

(2)若∠A=30°，AC=6，求⊙O的周长；

(3)在(2)的条件下，求阴影部分的面积.

Answer 1

【答案】(1)见解析；（2）⊙O的周长＝4π；（3）阴影面积为12-4π.

【解析】

（1）直接利用等腰三角形的性质结合切线的判定方法得出即可；

（2）直接利用锐角三角函数关系得出CO的长，再利用圆的周长公式求出即可;

（3）根据阴影面积=-求解即可．

(1)证明：连接OC.

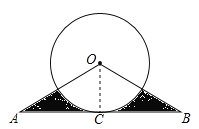
∵OA＝OB，CA＝CB，

∴OC⊥AB.

∴AB是⊙O的切线．

(2) ∵OA=OB，∠A=30°，AC=6，∠ACO=90°，

∴tan30°=，

∴CO=2，

∴⊙O的周长为：2π×2=4π．

（3）∵OA=OB，CA=CB. ∠A=30°，AC=6，

∴AB=12，∠AOB=120°

∴，

∴阴影面积为12-4π.