题目内容
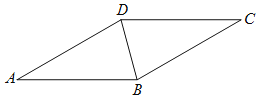
【题目】如图,BD是菱形ABCD的对角线.
(1)请用直尺和圆规作AB的垂直平分线EF,垂足为点E,交AD于点F;(不要求写作法,保留作图痕迹)
(2)在(1)的条件下,连接BF,若∠CBD=75°,求∠DBF的度数.
【答案】(1)见解析;(2)45°.
【解析】
(1)利用基本作图作EF垂直平分AB;
(2)利用菱形的性质得AD∥BC,∠ABD=∠CBD=75°,则∠ABC=150°,再利用平行线的性质得∠A=180°-∠ABC=180°-150°=30°,接着根据线段垂直平分线的性质得AF=BF,则∠A=∠FBA=30°,然后计算∠ABD-∠FBA即可.
解:(1)如图,EF为所作,
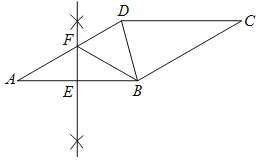
(2)∵四边形ABCD是菱形,
∴AD∥BC,∠ABD=∠CBD=75°,
∴∠ABC=150°,
∵AD∥BC,
∴∠A=180°-∠ABC=180°-150°=30°,
∵EF垂直平分AB,
∴AF=BF,
∴∠A=∠FBA=30°,
∴∠DBF=∠ABD-∠FBA=75°-30°=45°.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目