题目内容
【题目】如图,在数轴上点A表示数a,点B表示数b,点C表示数c,其中数b是最小的正整数,数a、c满足|a+2|+(c-6)2=0.若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.
(1)由题意可得:a= ,b= ,c= .
(2)若点A以每秒1个单位长度的速度沿数轴向左运动,点B和点C分别以每秒2个单位长度和3个单位长度的速度沿数轴向右运动,设点A、B、C同时运动,运动时间为t秒.
①当t=2时,分别求AC、AB的长度;
②在点A、B、C同时运动的过程中,3AC-4AB的值是否随着时间t的变化而变化?若变化,说明理由;若不变,求出3AC-4AB的值.
【答案】（1）-2，1，6；（2）①16，9；②在点A、B、C同时运动的过程中，3AC-4AB的值不随时间t的变化而变化，它的值为定值12.
【解析】
（1） 根据绝对值的非负性和偶数次方数的非负性，即可得出a，c的值，再由b时最小的正整数，即可得b的值.
（2） 用含有t的代数式分别表示AC、AB的长度，
①代入t=2，即可得到结果；
②AC、AB的代数式代入3AC-4AB中，即可得出结论.
（1）∵|a+2|+(c-6)2=0，b时最小的正整数，
∴a=-2，b=1，c=6；
（2）∵当时间为t秒时，A点表示的数为-t-2，B点表示的数为2t+1,C点表示的数为3t+6.
∴
，
①当t=2时，
，
，
②
，即，在点A、B、C同时运动的过程中，3AC-4AB的值不随时间t的变化而变化，它的值为定值12.
【题目】如图，有个形如六边形的点阵，它的中心是一个点，算第一层，第二层每边有两个点，第三层每边有三个点，依此类推．
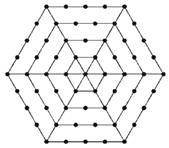
（1）填写下表：
层数 | 1 | 2 | 3 | 4 | 5 | 6 |
该层对应的点数 | 1 | 6 | _____ | 18 | _____ | _____ |
（2）写出第n层所对应的点数为_____；
（3）如果某一层共96个点，那么它是第_____层，此时所有层中共有_____个点．
