Question

【题目】如图，有个形如六边形的点阵，它的中心是一个点，算第一层，第二层每边有两个点，第三层每边有三个点，依此类推．

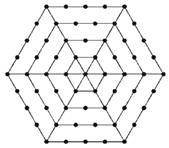
（1）填写下表：

层数	1	2	3	4	5	6
该层对应的点数	1	6	_____	18	_____	_____

（2）写出第n层所对应的点数为_____；

（3）如果某一层共96个点，那么它是第_____层，此时所有层中共有_____个点．

Answer 1

【答案】12 24 30 n＝1时有1个点，当n≥2时，有6(n﹣1)个点. 17 817

【解析】

（1）根据题目中的图形和题意，可以将表格中的数据补充完整；

（2）根据（1）中的结果可以解答本题；

（3）根据（2）中的结果可以解答本题．

（1）由图可知，第一层点的个数为：1，第二层点的个数为：6，第三层点的个数为：6+1×6=12，第四层，点的个数为：6+2×6=18，第五层点的个数为：6+3×6=24，第六层点的个数为：6+4×6=30，…，第n层，点的个数为：6+（n﹣2）×6=6（n﹣1）．

故答案为：12，24，30；

（2）由（1）可知，n=1时有1个点，当n≥2时，有6（n﹣1）个点．

故答案为：n=1时有1个点，当n≥2时，有6（n﹣1）个点；

（3）令6（n﹣1）=96，解得：n=17，此时所有层中共有：1+6+12+…+96=1+（6+96）×[（17﹣1）÷2]=817个点．

故答案为：17，817．