题目内容
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=8cm,BC=10cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.如果P、Q分别从A、B同时出发,当一个点到达终点时,另一个点随之停止.设运动时间为x秒,△PBQ的面积为ycm2.
(1)求y与x的函数关系式,写出x的取值范围;
(2)求运动多少秒时,△PBQ的面积为12cm2;
(3)求运动多少秒时,△PBQ的面有最大值.最大值是多少?

【答案】(1)y=﹣x2+8x(0<x<5);(2)当运动2秒时,△PBQ的面积为12cm2;(3)当x=4时,△PBQ的面有最大值.最大值是16.
【解析】试题分析:(1)根据题意用x表示出BP、BQ,根据三角形的面积公式计算;
(2)根据题意列出方程,解方程即可;
(3)根据二次函数的性质解答.
试题解析:解:(1)由题意得:AP=xcm,BQ=2xcm,则BP=(8﹣x)cm,y=![]() ×BQ×BP=x(8﹣x)=﹣x2+8x(0<x<5);
×BQ×BP=x(8﹣x)=﹣x2+8x(0<x<5);
(2)﹣x2+8x=12,x1=2,x2=6(不合题意,舍去),当运动2秒时,△PBQ的面积为12cm2;
(3)y=﹣x2+8x=﹣(x2﹣8x+16)+16=﹣(x﹣4)2+16,∴当x=4时,△PBQ的面有最大值.最大值是16.

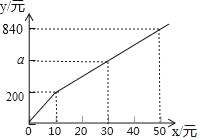
【题目】甲、乙两个批发店销售同一种苹果,甲批发店的价格为每千克6元.在乙批发店,一次购买数量不超过![]() 时,价格为每千克7元;一次购买数量超过
时,价格为每千克7元;一次购买数量超过![]() 时,其中有
时,其中有![]() 的价格为每千克7元,超过
的价格为每千克7元,超过![]() 部分的价格为每千克5元,设小王在同个批发店一次购买苹果的数量为
部分的价格为每千克5元,设小王在同个批发店一次购买苹果的数量为![]()
![]() .
.
(1)填表:
一次购买苹果的数量(单位: | 20 | 50 | 100 | … |
甲批发店花费(单位:元) | 300 | … | ||
乙批发店花费(单位:元) | 350 | … |
(2)分别用含![]() 的代数式表示甲、乙批发店所花费的钱数.
的代数式表示甲、乙批发店所花费的钱数.
(3)如果小王在同一个批发店一次购买苹果的数量为![]() ,通过计算说明他在甲、乙两个批批发店所花费的钱数少?
,通过计算说明他在甲、乙两个批批发店所花费的钱数少?
【题目】小林同学积极参加体育锻炼,天天坚持跑步,他每天以1000m为标准,超过的记作正数,不足的记作负数.下表是一周内小明跑步情况的记录(单位:m):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
跑步情况(m) | +420 | +460 | -100 | -210 | -330 | +200 | -240 |
(1)星期三小林跑了_____米
(2)小林在跑得最少的一天跑了______米?跑得最多的一天比最少的一天多跑了_____米?
(3)若小林跑步的平均速度为240米/分,求本周内小明用于跑步的时间.