Question

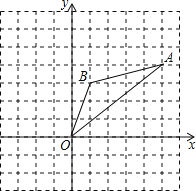
【题目】如图，⊙C经过原点且与两坐标轴分别交于点A和点B，点A的坐标为（0，3），D为⊙C在第一象限内的一点且∠ODB=60°．

求：（1）求线段AB的长及⊙C的半径；

（2）求B点坐标及圆心C的坐标．

Answer 1

【答案】（1）6，3；（2）（3，0），（，）

【解析】

（1）在Rt△OAB中，只要证明∠OAB=∠ODB=60°，利用直角三角形30度角性质即可解决问题．

（2）过C点作CE⊥OB于E，利用直角三角形30度角性质求出OB的长，再利用垂径定理以及三角形中位线定理求出CE即可解决问题．

（1）∵点A的坐标为（0，3），∴OA=3．

∵∠ODB=∠OAB，∠ODB=60°，∴∠OAB=60°．

∵∠AOB是直角，∴AB是⊙C的直径，∴∠OBA=30°，∴AB=2OA=6，∴⊙C的半径r=3；

（2）过C点作CE⊥OB于E．在Rt△OAB中，∠OBA=30°，∴OB=AB=×6=3，∴B的坐标为：（3，0），由垂径定理得：OE=OB=．

∵AC=BC，OE=BE，∴CE=OA=×3=，∴C的坐标为（）．