题目内容
【题目】如图,已知AB、AD是⊙O的弦,点C是DO的延长线与弦AB的交点,∠ABO=30°,OB=2.
(1)求弦AB的长;
(2)若∠D=20°,求∠BOD的度数.
【答案】
(1)解:过点O作OE⊥AB于点E,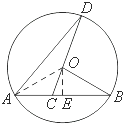
∵在Rt△OEB中,OB=2,∠B=30°,
∴BE=OBcos30°=2× ![]() =
= ![]() ,
,
∴AB=2BE=2 ![]()
(2)解:连接OA,
∵OA=OB=OD,∠B=30°,∠D=20°,
∴∠OAB=∠B=30°,∠OAD=∠D=20°,
∴∠BAD=∠OAB+∠OAD=30°+20°=50°,
∴∠BOD=2∠BAD=100°
【解析】(1)可作弦心距,构造直角三角形,先求出一半,再求出整条弦长;(2)连接半径,转化∠OAB=∠B,∠OAD=∠D,进而∠BOD=2∠BAD=100°.

练习册系列答案
相关题目