题目内容
已知抛物线y=-
x2-x+m与x轴有两个不同的交点A、B,抛物线的顶点为C.求是否存在实数m,使△ABC为等腰直角三角形?若存在,求出m的值;若不存在,请说明理由.
| 3 | 4 |
分析:令y=0,得到关于x的一元二次方程,求出两根之和与两根之积表达式,然后求出AB的距离,求出函数的顶点坐标,利用等腰直角三角形的性质,令顶点纵坐标的绝对值等于AB的一半即可得到关于m的方程.若能求出m的值,则m的值存在,否则不存在.
解答:解:设A、B的坐标为(x1,0),(x2,0),
由-
x2-x+m=0,有x1+x2=-
,x1•x2=-
m,
∴|AB|=|x1-x2|=
=
=
,
又∵-
=-
=-
,
=
,
∴顶点C的坐标为(-
,
),
∵△ABC是等腰直角三角形,
∴|
|=
|AB|=
,
∴m=1.
由-
| 3 |
| 4 |
| 4 |
| 3 |
| 4 |
| 3 |
∴|AB|=|x1-x2|=
| (x1+x2)2-4x1x2 |
|
| 4 |
| 3 |
| 1+3m |
又∵-
| b |
| 2a |
| -1 | ||
2×(-
|
| 2 |
| 3 |
| 4ac-b2 |
| 4a |
| 3m+1 |
| 3 |
∴顶点C的坐标为(-
| 2 |
| 3 |
| 3m+1 |
| 3 |
∵△ABC是等腰直角三角形,
∴|
| 3m+1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 3m+1 |
∴m=1.
点评:本题考查了二次函数综合题,涉及函数与方程的关系、等腰直角三角形的性质、二次函数的最值等,要综合分析,认真解答.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
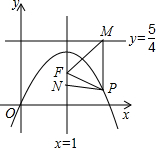 值,若不存在请说明理由.
值,若不存在请说明理由.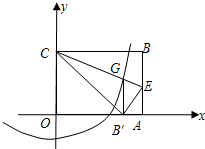 半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标.
半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标.