题目内容
已知抛物线C1、C2关于x轴对称,抛物线C1、C3关于y轴对称,如果C2的解析式为y=-| 3 | 4 |
分析:抛物线C1、C2关于x轴对称,顶点也关于x轴对称,开口方向相反,a的符号相反,由顶点式直接写出C1解析式;
抛物线C1、C3关于y轴对称,顶点也关于y轴对称,开口方向相同,a的符号相同,由顶点式直接写出C3解析式.
抛物线C1、C3关于y轴对称,顶点也关于y轴对称,开口方向相同,a的符号相同,由顶点式直接写出C3解析式.
解答:解:根据顶点的对称性,抛物线的开口方向解题,C2顶点坐标为(2,1),
∵抛物线C1、C2关于x轴对称,
∴C1的顶点坐标为(2,-1),a=
,
C1解析式为y=
(x-2)2-1,
又∵抛物线C1、C3关于y轴对称,
∴C3的顶点坐标为(-2,-1),a=
,
C3解析式为y=
(x+2)2-1.
∵抛物线C1、C2关于x轴对称,
∴C1的顶点坐标为(2,-1),a=
| 3 |
| 4 |
C1解析式为y=
| 3 |
| 4 |
又∵抛物线C1、C3关于y轴对称,
∴C3的顶点坐标为(-2,-1),a=
| 3 |
| 4 |
C3解析式为y=
| 3 |
| 4 |
点评:若关于x轴对称,则横坐标不变,纵坐标变为相反数;若关于y轴对称,则纵坐标不变,横坐标变为相反数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
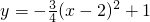 ,则C3的解析式为________.
,则C3的解析式为________. ,则C3的解析式为 .
,则C3的解析式为 . ,则C3的解析式为 .
,则C3的解析式为 .