题目内容
【题目】某公司新研发一种办公室用壁挂式电磁日历,底板是一块长方形磁块,再用31枚圆柱形小铁片标上数字吸附在底板上作为日期,如图1是2007年10月份日历
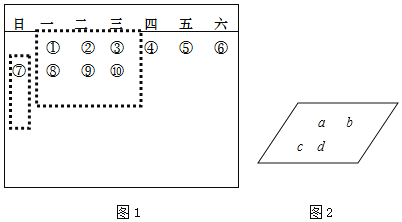
(1)用长方形和正方形分别圈出相邻的3个数和9个数,若设圈出的数的中心数为a,用含a的整式表示这3个数的和与9个数的和,结果分别为 , .
(2)用某种图形圈出相邻的5个数,使这5个数的和能表示成5a的形式,请在图2中画出一个这样的图形.
(3)用平行四边形圈出相邻的四个数,是否存在这样的4个数使得a+b+c+d=114?如果存在就求出来,不存在说明理由.
(4)第一次翻动31枚日历铁片,第二次翻动其中的30枚,第三次翻动其中的29枚,……,第31次只翻动其中的一枚,按这样的方法翻动日历铁片,能否使铁板上所有的31枚铁片原来有数字的一面都朝下,试通过计算证明你的判断.
【答案】(1)3a,9a;(2)见解析;(3)不存在,理由见解析;(4)不能,证明见解析
【解析】
(1)根据日历的特点可列出关于a的方程,求解即可;
(2)根据上下左右的数量关系,画图即可;
(3)举例拆分即可.
(4)根据数字的奇偶性规律验证.
(1)长方形中中间数为a,上下两数分别为(a﹣7);(a+7)
∴3个数的和为a+(a﹣7)+(a+7)=3a
正方形中中间数为a,那么左右两数分别为(a﹣1);(a+1)
根据以上规律左边三个数的和为3(a﹣1);中间三个数的和为3a;右边三个数的和为3(a+1)
∴9个数的和为3(a﹣1)+3a+3(a+1)=9a
故答案为:3a,9a.
(2)如图所示即可
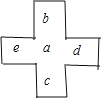
(3)不存在,
根据图形的规律得,b=a+1,c=a+6,d=a+7,
∵a+b+c+d=114,
∴a+a+1+a+6+a+7=114,
a=25,
∴d=a+25=32,
∴不存在这样的4个数使得a+b+c+d=114.
(4)不能,
共翻动了![]() (次),
(次),
而要使一个铁皮翻面,需要奇数次,
所有的31枚铁片原来有数字的一面都朝下需要31 ![]() 奇数次,
奇数次,
∵496不是奇数,
∴第一次翻动31枚日历铁片,第二次翻动其中的30枚,第三次翻动其中的29枚,……,第31次只翻动其中的一枚,按这样的方法翻动日历铁片,不能使铁板上所有的31枚铁片原来有数字的一面都朝下.