题目内容
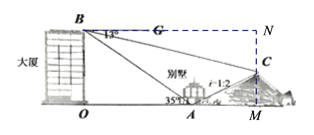
【题目】如图所示,在同一水平面从左到右依次是大厦、别墅、小山、小彬为了测得小山的高度,在大厦的楼顶B处测得山顶C的俯角∠GBC=13°,在别墅的大门A点处测得大厦的楼顶B点的仰角∠BAO=35°,山坡AC的坡度i=1:2,OA=500米,则山C的垂直高度约为( )(参考数据:sin13°≈0.22,tan13°≈0.23,sin35°≈0.57)

A. 161.0 B. 116.4 C. 106.8 D. 76.2
【答案】A
【解析】分析:分别过点C作CM⊥OA,CN⊥BG,垂足为点M,N,构建Rt△ABO,Rt△ACM,Rt△BCN,利用三角形函数的定义列方程求解.
详解:分别过点C作CM⊥OA,CN⊥BG,垂足为点M,N.
Rt△ABO中,BO=OAtan35°≈0.7×500=350.
设MC=x,则AM=2x,所以BN=OM=500+2x,CN=350-x.
Rt△BCN中,CN=BNtan13°,即350-x=0.23(500+2x),解得x≈161.0米.
故选A.

练习册系列答案
相关题目