题目内容
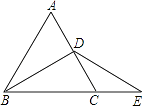
【题目】如图,△ABC中,∠ACB=90°,tanA= ![]() ,点D是边AC上一点,连接BD,并将△BCD沿BD折叠,使点C恰好落在边AB上的点E处,过点D作DF⊥BD,交AB于点F.
,点D是边AC上一点,连接BD,并将△BCD沿BD折叠,使点C恰好落在边AB上的点E处,过点D作DF⊥BD,交AB于点F.
(1)求证:∠ADF=∠EDF;
(2)探究线段AD,AF,AB之间的数量关系,并说明理由;
(3)若EF=1,求BC的长.
【答案】
(1)
证明:∵DF⊥DB,
∴∠BDF=90°,
∴∠ADF+∠BDC=∠EDF+∠BDE=90°,
由折叠性质得:∠BDE=∠BDC,
∴∠ADF=∠EDF;
(2)
解:AD,AF,AB之间的数量关系为AD2=AFAB,理由如下:
由折叠性质得:∠DEF=∠BDF=∠C=90°,
∴∠EDF+∠DFE=∠ABD+∠DFE=90°,
∴∠EDF=∠ABD,
∴∠ADF=∠DBA,
∵∠A=∠A,
∴△ADF∽△ABD,
∴AF:AD=AD:AB,
∴AD2=AFAB;
(3)
解:在Rt△ADE中,tanA=DE:AE= ![]() :1,
:1,
设AE=x,则DE= ![]() x,
x,
由勾股定理得:AD= ![]() =
= ![]() =
= ![]() x,
x,
∵∠ABD=∠EDF,∠AED=∠DEF,
∴△BDE∽△DFE,
∴DE:EF=BE:DE,即DE2=EFEB,
∴( ![]() x)2=1×BE,即BE=2x2,
x)2=1×BE,即BE=2x2,
由(2)知AD2=AFAB,
∴( ![]() x)2=(AE﹣EF)(AE+BE)=(x﹣1)×(x+2x2),
x)2=(AE﹣EF)(AE+BE)=(x﹣1)×(x+2x2),
即3x2=(x﹣1)×(x+2x2),
解得:x=1+ ![]() ,x=1﹣
,x=1﹣ ![]() (不合题意舍去),
(不合题意舍去),
∴BE=2x2=2(1+ ![]() )2=5+2
)2=5+2 ![]() ,
,
由折叠可知,BC=BE=5+2 ![]() .
.
【解析】(1)由已知可得∠ADF+∠BDC=∠EDF+∠BDE=90°,再由折叠的性质得∠BDE=∠BDC,即可得出结论;(2)由折叠的性质与已知得∠DEF=∠BDF=∠C=90°,推出∠EDF+∠DFE=∠ABD+∠DFE=90°,得出∠EDF=∠ABD,∠ADF=∠DBA,证得△ADF∽△ABD,对应边成比例即可得出结果;(3)在Rt△ADE中,tanA=DE:AE= ![]() :1,设AE=x,则DE=
:1,设AE=x,则DE= ![]() x,由勾股定理可解得AD=
x,由勾股定理可解得AD= ![]() x,证得△BDE∽△DFE,得出DE2=EFEB,解得BE=2x2 , 再由(2)知AD2=AFAB,即(
x,证得△BDE∽△DFE,得出DE2=EFEB,解得BE=2x2 , 再由(2)知AD2=AFAB,即( ![]() x)2=(AE﹣EF)(AE+BE)=(x﹣1)×(x+2x2),解得x的值,即可得出结果.
x)2=(AE﹣EF)(AE+BE)=(x﹣1)×(x+2x2),解得x的值,即可得出结果.
【考点精析】掌握勾股定理的概念和翻折变换(折叠问题)是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

【题目】某校为了了解九年级学生(共450人)的身体素质情况,体育老师对九(1)班的50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制了如下部分频数分布表和部分频数分布直方图.
组别 | 次数x | 频数(人数) |
A | 80≤x<100 | 6 |
B | 100≤x<120 | 8 |
C | 120≤x<140 | m |
D | 140≤x<160 | 18 |
E | 160≤x<180 | 6 |

请结合图表解答下列问题:
(1)表中的m=;
(2)请把频数分布直方图补完整;
(3)这个样本数据的中位数落在第组;
(4)若九年级学生一分钟跳绳次数(x)合格要求是x≥120,则估计九年级学生中一分钟跳绳成绩不合格的人数.