题目内容
【题目】已知,如图1,△ABC中,BA=BC,D是平面内不与A、B、C重合的任意一点,∠ABC=∠DBE,BD=BE. 
(1)求证:△ABD≌△CBE;
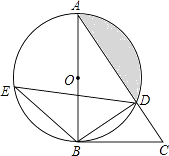
(2)如图2,当点D是△ABC的外接圆圆心时,请判断四边形BDCE的形状,并证明你的结论.
【答案】
(1)证明:∵∠ABC=∠DBE,
∴∠ABC+∠CBD=∠DBE+∠CBD,
∴∠ABD=∠CBE,
在△ABD与△CBE中,
∵ 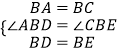 ,
,
∴△ABD≌△CBE(SAS)
(2)解:四边形BDCE是菱形.证明如下:
同(1)可证△ABD≌△CBE,
∴CE=AD,
∵点D是△ABC外接圆圆心,
∴DA=DB=DC,
又∵BD=BE,
∴BD=BE=CE=CD,
∴四边形BDCE是菱形
【解析】(1)由∠ABC=∠DBE可知∠ABC+∠CBD=∠DBE+∠CBD,即∠ABD=∠CBE,根据SAS定理可知△ABD≌△CBE;(2)由(1)可知,△ABD≌△CBE,故CE=AD,根据点D是△ABC外接圆圆心可知DA=DB=DC,再由BD=BE可判断出BD=BE=CE=CD,故可得出四边形BDCE是菱形.
【考点精析】利用菱形的判定方法和三角形的外接圆与外心对题目进行判断即可得到答案,需要熟知任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形;过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心.

练习册系列答案
相关题目