题目内容
【题目】如图,在△ABC中,以AB为直径的⊙O交AC于点D,直径AB左侧的半圆上有一点动点E(不与点A、B重合),连结EB、ED.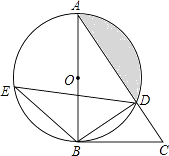
(1)如果∠CBD=∠E,求证:BC是⊙O的切线;
(2)当点E运动到什么位置时,△EDB≌△ABD,并给予证明;
(3)在(1)的条件下,若tanE= ![]() ,BC=
,BC= ![]() ,求阴影部分的面积.(计算结果精确到0.1)
,求阴影部分的面积.(计算结果精确到0.1)
(参考数值:π≈3.14, ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)
【答案】
(1)
证明:∵AB为⊙O的直径,
∴∠ADB=90°,
即∠ABD+∠BAD=90°.
又∵∠CBD=∠E,∠BAD=∠E,
∴∠ABD+∠CBD=90°,即∠ABC=90°.
∴BC⊥AB.
∴BC是⊙O的切线.
(2)
证明:当点E运动到DE经过点O位置时,△EDB≌△ABD.证明如下:
当点E运动到DE经过点O位置时,∠EBD=∠ADB=90°,
在△EDB与△ABD中,
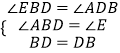 ,
,
∴△EDB≌△ABD(AAS).
(3)
解:如图,连接OD,过点O作OF⊥AD于点F,
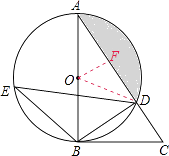
∵∠BAD=∠E,tanE= ![]() ,
,
∴tan∠BAD= ![]() .
.
又∵∠ADB=90°,
∴∠BAD=30°.
∵∠ABC=90°,BC= ![]() ,
,
∴AB= ![]() =4.
=4.
∴AO=2,OF=1,AF=AOcos∠BAD= ![]() .
.
∴AD=2 ![]() .
.
∵AO=DO,
∴∠AOD=120°.
∴S阴影=S扇形OAD﹣S△AOD= ![]() ﹣
﹣ ![]() ×3=2
×3=2 ![]() ×1=
×1= ![]() π﹣
π﹣ ![]() ≈2.5.
≈2.5.
【解析】(1)欲证明BC是⊙O的切线,只需证得BC⊥AB;(2)利用圆周角定理,全等三角形的判定定理AAS证得当点E运动到DE经过点O位置时,△EDB≌△ABD;(3)如图,连接OD,过点O作OF⊥AD于点F.S阴影=S扇形OAD﹣S△AOD . 由圆周角定理和正切三角函数定义易求AB的长度、圆心角∠AOD=120°.所以根据扇形面积公式和三角形的面积公式进行计算即可.
【考点精析】解答此题的关键在于理解切线的判定定理的相关知识,掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线,以及对扇形面积计算公式的理解,了解在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).