题目内容
【题目】如图,已知动点A在函数 ![]() 的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x,y轴分别于点P,Q.当QE:DP=4:9时,图中阴影部分的面积等于 .
的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x,y轴分别于点P,Q.当QE:DP=4:9时,图中阴影部分的面积等于 . 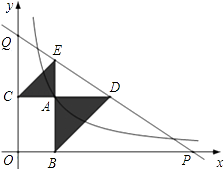
【答案】![]()
【解析】解: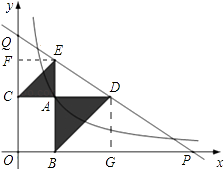
解法一:过点D作DG⊥x轴于点G,过点E作EF⊥y轴于点F.
令A(t, ![]() ),则AD=AB=DG=
),则AD=AB=DG= ![]() ,AE=AC=EF=t.
,AE=AC=EF=t.
在直角△ADE中,由勾股定理,得DE= ![]() =
= ![]() =
= ![]() =
= ![]() .
.
∵△EFQ∽△DAE,
∴QE:DE=EF:AD,
∴QE= ![]() ,
,
∵△ADE∽△GPD,
∴DE:PD=AE:DG,
∴DP= ![]() .
.
又∵QE:DP=4:9,
∴ ![]() :
: ![]() =4:9,
=4:9,
解得t2= ![]() .
.
∴图中阴影部分的面积= ![]() AC2+
AC2+ ![]() AB2=
AB2= ![]() t2+
t2+ ![]() ×
× ![]() =
= ![]() +3=
+3= ![]() ;
;
解法二:∵QE:DP=4:9,
∴EF:PG=4:9,
设EF=4t,则PG=9t,
∴A(4t, ![]() ),
),
由AC=AE AD=AB,
∴AE=4t,AD= ![]() ,DG=
,DG= ![]() ,GP=9t,
,GP=9t,
∵△ADE∽△GPD,
∴AE:DG=AD:GP,
4t: ![]() =
= ![]() :9t,即t2=
:9t,即t2= ![]() ,
,
图中阴影部分的面积= ![]() ×4t×4t+
×4t×4t+ ![]() ×
× ![]() ×
× ![]() =
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】利用反比例函数的性质对题目进行判断即可得到答案,需要熟知性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.

【题目】温州享有“中国笔都”之称,其产品畅销全球,某制笔企业欲将n件产品运往A,B,C三地销售,要求运往C地的件数是运往A地件数的2倍,各地的运费如图所示.设安排x件产品运往A地. 
(1)当n=200时,①根据信息填表:
A地 | B地 | C地 | 合计 | |
产品件数(件) | x | 2x | 200 | |
运费(元) | 30x |
②若运往B地的件数不多于运往C地的件数,总运费不超过4000元,则有哪几种运输方案?
(2)若总运费为5800元,求n的最小值.