题目内容
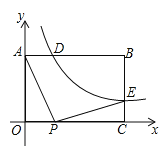
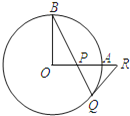
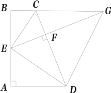
【题目】如图，已知四边形ABCD中，AB⊥AD，BC∥AD，E为AB的中点，且EC、ED分别为∠BCD、∠ADC的角平分线，EF⊥CD交BC的延长线于点G，连接DG.
（1）求证：CE⊥DE；
（2）若AB=6，求CF·DF的值；
（3）当△BCE与△DFG相似时，
的值是 .
【答案】（1）证明见解析；（2）CF·DF的值为9；（3）
的值为
或
【解析】
(1)利用平行线及角平分线的性质即可证明；
（2）可证△CFE∽△EFD，可得
，变形得
由角平分线性质可得
FF=EA=3，代入即可得结论
（3）分类讨论：若△BCE∽△FDG，可证△BCE≌△FEC、△ADE≌△FED，过G作GH⊥AD于H可证△BCE∽△HDG可得
即可得
；当△BCD∽△FGD时可证△CFE≌△CFG可推出∠1=60°，∠4=30°在Rt△BCE中 
，在Rt△ADE中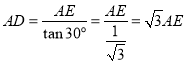
即可得
的值.
(1)证明：
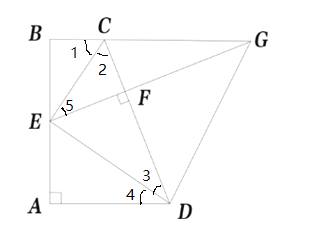
∵BC∥AD
∴∠BCD+∠ADC=180°
∵EC、ED分别平分∠BCD、∠ADC
∴∠1=∠2，∠3=∠4，∠1+∠2+∠3+∠4=180°
∴∠2+∠3=90° ∴∠CED=90°
∴CE⊥DE
(2)∵CE⊥DE，EF⊥CD
∴∠2+∠5=90°，∠2+∠3=90°
∴∠5=∠3
∴△CFE∽△EFD
∴
∴
∵ED平分∠FDA，∠A=∠EFD=90°
∴FF=EA
∵E为AB中点，AB=6
∴FE=AE=BE=3
∴
(3) 若△BCE∽△FDG
∴∠1=∠FDG
∵∠1=∠2
∴∠2=∠FDG
∴EC∥CD
∴
∵∠1=∠2，∠EBC=∠CFE=90°，EC=EC
∴△BCE≌△FCE
∴BC=CF
∵∠3=∠4，∠A=∠EFD=90°，ED=ED
∴△ADE≌△FDE
∴AD=FD
∴
∴
过G作GH⊥AD于H
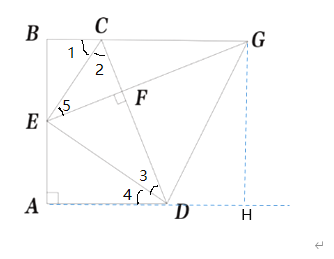
∴∠DHG=90°
∵∠3=∠4，∠FDG=∠2
又∵∠3+∠4+∠FDG+∠GDH=180°
∠3+∠4+∠1+∠2=180°
∴∠GDH=∠1
又∵∠GFD=∠B=90°
∴△BCE∽△HDG
∴
∵
∴
∴
∴
∴
当△BCD∽△FGD
∴∠GDF=∠BEC
∴∠BEC=∠5=∠3=∠4
∵FD=FD，∠3=∠FDG，∠EFD=∠GFD
∴△EDF≌△GFD
∴EF=FG
∵FD⊥EG
∴∠EFC=∠GFC=90°
又∵CF=CF
∴△CFE≌△CFG
∴∠2=∠GCD
∴∠1=∠2=∠GCD
∵∠1+∠2+∠GCD=180°
∴∠1=60°
∴∠4=30°
在Rt△BCE中 
在Rt△ADE中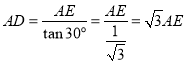
∴
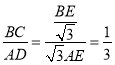
综上所述的值为或
