Question

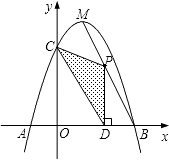
【题目】如图，△ABC和△DEF均是边长为4的等边三角形，△DEF的顶点D为△ABC的一边BC的中点，△DEF绕点D旋转，且边DF,DE始终分别交△ABC的边AB，AC于点H，G，图中直线BC两侧的图形关于直线BC成轴对称．连结HH′,HG,GG′,H′G′，其中HH′、GG′分别交BC于点I，J．

（1）求证：△DHB∽△GDC；
（2）设CG=x，四边形HH′G′G的面积为y，
①求y关于x的函数解析式和自变量x的取值范围．
②求当x为何值时，y的值最大，最大值为多少？

Answer 1

【答案】
（1）

证明：在正△ABC中，∠ABC=∠ACB=60°，

∴∠BHD+∠BDH=120°，

在正△DEF中，∠EDF=60°，

∴∠GDC+∠BDH=120°，

∴∠BHD=∠GDC，

∴△DHB∽△GDC

（2）

证明：①∵D为BC的中点，

∴BD=CD=2，

由△DHB∽△GDC，

∴ ，

即： ，

∴BH= ，

∵H，H′和G，G′关于BC对称，

∴HH′⊥BC，GG′⊥BC，

∴在Rt△BHI中，BI= BH= ，HI= BH= ，

在Rt△CGJ中，CJ= CG= ，GJ= CG= ，

∴HH′=2HI= ，GG’=2GJ= x，IJ=4﹣ ﹣ ，

∴y= （ + x）（4﹣ ﹣ ）

∵边DF、DE始终分别交△ABC的边AB、AC于点H、G，

∴当△DEF绕点D旋转时，点H和A重合时，AG=3，

∴x=CG=1，

当点G和A重合时，CG=4，

∴x=4，

∴1≤x≤4

②由①得，y=﹣ （ +x）2+2 （ +x），

设 =a，得y=﹣ a2+2 a，

当a=4时，y最大=4 ，

此时 =4，解得x=2．

【解析】（1）由等边三角形的特点得到相等关系，即可；（2）由相似三角形得到 ，再结合对称，表示出相关的线段，四边形HH′G′G的面积为y求出即可．