Question

【题目】如图，在正方形ABCD中，△BPC是等边三角形，BP、CP的延长线分别交AD于点E、F，连接BD、DP，BD与CF相交于点H．给出下列结论：
①△ABE≌△DCF；② ；③DP2=PHPB；④ ．
其中正确的是 ． （写出所有正确结论的序号）

Answer 1

【答案】①③
【解析】解：①∵△BPC是等边三角形，
∴BP=PC=BC，∠PBC=∠PCB=∠BPC=60°，
∵四边形ABCD为正方形，
∴AB=BC=CD，∠A=∠ADC=∠BCD=90°
∴∠ABE=∠DCF=30°，
在△ABE与△CDF中，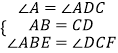
，
∴△ABE≌△DCF（ASA），
故①正确；
②∵PC=CD，∠PCD=30°，
∴∠PDC=75°，
∴∠FDP=15°，
∵∠DBA=45°，
∴∠PBD=15°，
∴∠FDP=∠PBD，
∵∠DFP=∠FCB=∠BPC=60°，
∴△DFP∽△BPH，
∴ = = =tan∠DCF= ，
故②错误；
③∵∠FDP=15°，
∴∠PDH=30°
∴∠PDH=∠PCD，
∵∠DPH=∠DPC，
∴△DPH∽△CDP，
∴ = ，
∴DP2=PHCD，
∵PB=CD，
∴DP2=PHPB，
故③正确；
④设正方形ABCD的边长是3，
∵△BPC为正三角形，
∴∠PBC=60°，PB=BC=AD=3，
∴∠EBA=30°，
∴AE=ABtan30°=3× = ，
BE= = =2 ，
∴EP=BE﹣BP=2 ﹣3，
S△BED=SABD﹣SABE= ×3×3﹣ ×3× = ，
S△EPD= S△BED= × = ，
∴ = = ，
故④错误；
∴正确的是①③；
故答案为：①③．
①根据等边三角形的性质和正方形的性质，得到∠ABE=∠DCF，∠A=∠ADC，AB=CD，证得△ABE≌△DCF，①正确；
②由于∠FDP=∠PBD，∠DFP=∠BPC=60°，推出△DFP∽△BPH，得到 = = =tan∠DCF= ，②错误；
③由于∠PDH=∠PCD=30°，∠DPH=∠DPC，推出△DPH∽△CPD，得到 = ，PB=CD，等量代换得到DP2=PHPB，③正确；
④设正方形ABCD的边长是3，则PB=BC=AD=3，求得∠EBA=30°，得出AE、BE、EP的长，由S△BED=SABD﹣SABE ， S△EPD= S△BED ， 求得 = ，④错误；即可得出结论．