题目内容
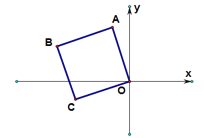
【题目】(2016湖北省荆州市第23题)如图,A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作OF的平行线交AB的延长线于点D,延长AF交直线CD于点H.
(1)求证:CD是半圆O的切线;
(2)若DH=6﹣3![]() ,求EF和半径OA的长.
,求EF和半径OA的长.
【答案】(1)、证明过程见解析;(2)、EF=2-![]() ;OA=2.
;OA=2.
【解析】
试题分析:(1)、连接OB,根据已知条件得到△AOB是等边三角形,得到∠AOB=60°,根据圆周角定理得到∠AOF=∠BOF=30°,根据平行线的性质得到OC⊥CD,由切线的判定定理即可得到结论;(2)、根据平行线的性质得到∠DBC=∠EAO=60°,解直角三角形得到BD=![]() BC=
BC=![]() AB,推出AE=
AB,推出AE=![]() AD,根据相似三角形的性质得到
AD,根据相似三角形的性质得到![]() ,求得EF=2﹣
,求得EF=2﹣![]() ,根据直角三角形的性质即可得到结论.
,根据直角三角形的性质即可得到结论.
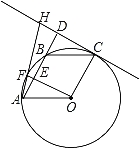
试题解析:(1)、连接OB, ∵OA=OB=OC, ∵四边形OABC是平行四边形, ∴AB=OC,
∴△AOB是等边三角形, ∴∠AOB=60°, ∵∠FAD=15°, ∴∠BOF=30°, ∴∠AOF=∠BOF=30°,
∴OF⊥AB, ∵CD∥OF, ∴CD⊥AD, ∵AD∥OC, ∴OC⊥CD, ∴CD是半圆O的切线;
(2)、∵BC∥OA, ∴∠DBC=∠EAO=60°, ∴BD=![]() BC=
BC=![]() AB, ∴AE=
AB, ∴AE=![]() AD, ∵EF∥DH,∴△AEF∽△ADH,
AD, ∵EF∥DH,∴△AEF∽△ADH,
∴![]() , ∵DH=6﹣3
, ∵DH=6﹣3![]() , ∴EF=2﹣
, ∴EF=2﹣![]() , ∵OF=OA, ∴OE=OA﹣(2﹣
, ∵OF=OA, ∴OE=OA﹣(2﹣![]() ),
),
∵∠AOE=30°, ∴![]() =
=![]() =
=![]() , 解得:OA=2.
, 解得:OA=2.

练习册系列答案
相关题目