题目内容
【题目】(2016广东省梅州市第20题)
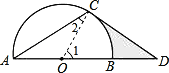
如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.

【答案】(1)、证明过程见解析;(2)、![]()
【解析】
试题分析:(1)、连接OC,根据等腰三角形的性质得出∠CAD=∠D=30°,根据OA=OC得出∠2=∠CAD =30°,从而得出∠OCD=∠ACD —∠ACO=90°;(2)、首先求出扇形BOC的面积,根据Rt△OCD的三角函数得出CD的长度,从而求出Rt△OCD的面积,然后求出阴影部分的面积.
试题解析:(1)、连接OC. ∵AC=CD,∠ACD=120°, ∴∠CAD=∠D=30°.
∵OA=OC, ∴∠2=∠CAD =30°.(或 ∠ACO=∠CAD=30° )
∴∠OCD=∠ACD —∠ACO=90°,即OC⊥CD. ∴CD是⊙O的切线.
(2)、由(1)知∠2=∠CAD =30°.(或 ∠ACO=∠CAD=30° ), ∴∠1=60°.(或∠COD =60°)
∴![]() . 在Rt△OCD中,∵
. 在Rt△OCD中,∵![]() ,
,![]() ∴
∴![]() .
.
∴![]() ∴图中阴影部分的面积为
∴图中阴影部分的面积为![]()

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目