题目内容
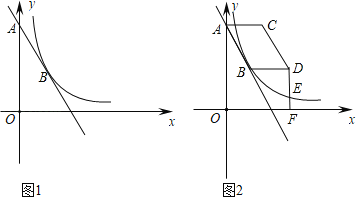
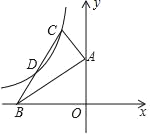
【题目】如图坐标系中,Rt△BAC的直角顶点A在y轴上,顶点B在x轴上,且OA=4,OB=6,双曲线y=![]() 经过点和斜边BC的中点D,则k=_____.
经过点和斜边BC的中点D,则k=_____.
【答案】﹣14.
【解析】
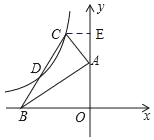
过点C作CE⊥y轴于E点,设D(m,n).因为点C、D均在双曲线上,则2n(2m+6)=mn①,又因为∠CAB=90°,所以△CEA∽△AOB,根据相似三角形的性质可得![]() ,则6(﹣2m﹣6)=4(2n﹣4)②,联立①②,计算得到 m=﹣4,n=﹣
,则6(﹣2m﹣6)=4(2n﹣4)②,联立①②,计算得到 m=﹣4,n=﹣![]() ,即可得到k.
,即可得到k.
解:过点C作CE⊥y轴于E点.设D(m,n),则C(2m+6,2n)、E(0,2n)
EA=2n﹣4,CE=﹣2m﹣6,
∵点C、D均在双曲线上,
∴2n(2m+6)=mn①,
∵∠CAB=90°,
∴△CEA∽△AOB,
∴![]() ,
,
即CEOB=AEOA,
∴6(﹣2m﹣6)=4(2n﹣4)②,
联立①②,解得 m=﹣4,n=﹣![]() ,
,
∴k=﹣4×![]() =﹣14.
=﹣14.
故答案为﹣14.

练习册系列答案
相关题目