Question

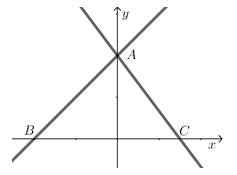
【题目】如图，在平面直角坐标系中，直线y=x+4与y轴交于点A，与x轴交于点B，直线y=kx+b经过点A，且交x轴与点C(3，0)．

（1）求直线AC的函数表达式；

（2）动点P在线段CB上由C向B匀速运动，到达点B后停止运动，运动速度为3个单位长度，过点P作PE⊥x轴，交直线AC于点E，过点E作直线GE∥x轴交轴于点F，交直线AB于点G，设点P的运动时间为t(t＞0)秒．

①直接写出线段PE的长度(用含t的代数式表示)；

②当EG=1时，请直接写出t的值．

Answer 1

【答案】（1）；（2）①4t；②或．

【解析】

（1）根据直线AB的解析式y=x+4，求出点A的坐标，然后即可利用待定系数法求出直线AC的解析式；

（2）先根据已知条件求出点P坐标，点E和点P的横坐标相同，所以再将E点的横坐标代入AC解析式，即可求出PE的长；

（3）先根据现有条件表示出G点坐标，再分成当E点在第一象限和E点在第二象限两种情况讨论即可．

（1）∵点A在y=x+4上，

∴A的坐标为（0，4），

将A（0，4），C（3，0）代入AC的解析式y=kx+b，

得，

解得，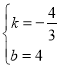

∴AC的解析式为y=x+4；

（2）如图：

∵AB的解析式为y=x+4，

∴B的坐标为（-4，0），A的坐标为（0，4），

∴OB=4，OC=3，

∵CP=3t，

∴OP=OC-CP=3-3t，

∴P的坐标为（3-3t，0），

∵PE⊥x轴，

∴点E的横坐标为3-3t，

∵点E在y=x+4上，

∴y=（3-3t）+4=4t，

∴PE的长为4t；

（3）∵GE∥x轴，

∴G的纵坐标为4t，

又∵G在y=x+4上，

∴4t=x+4，

解得x=4t-4，

∴G点的坐标为（4t-4，4t），

①如图，

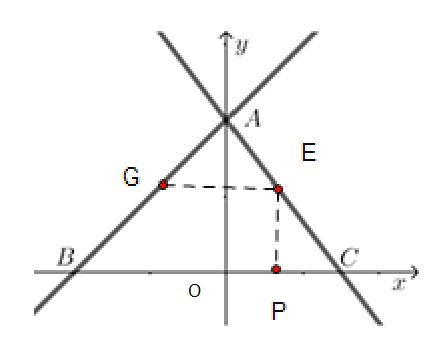
当E点在第一象限时，EG=3t-3-（4-4t）=1，

解得t=；

②如图，

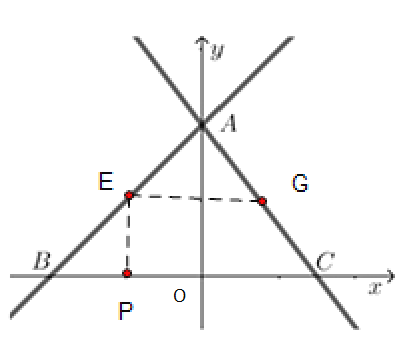
当E点在第二象限时，EG=3-3t-（4t-4）=1，

解得t=；

综上，t的值为或．