题目内容
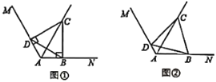
【题目】已知射线AC是∠MAN的角平分线, ∠NAC=60°, B, D分别是射线AN. AM上的点,连接BD.
(1)在图①中,若∠ABC=∠ADC=90°,求∠CDB的大小;
(2)在图②中,若∠ABC+∠ADC=180°,求证:四边形ABCD的面积是个定值.
【答案】(1)∠CDB=60°.(2)见解析
【解析】
(1)利用四边形的内角和即可得出∠BCD的度数,再利用角平分线的性质定理即可得出CD=CB,△BCD是等边三角形,即可求解;
(2)先判断出∠CDE=∠ABC,进而得出△CDE≌△CBF(AAS),再根据分割面积法证明四边形ABCD的面积是定值即可.
(1)∵射线AC是∠MAN的角平分线,∠NAC=60°,
∴∠MAN=120°,
∵∠ABC=∠ADC=90°,
根据四边形的内角和得,∠BCD=360°(∠ABC+∠ADC+∠MAN)=60°,
∵AC是∠MAN的平分线,CD⊥AM.CB⊥AN,
∴CD=CB(角平分线的性质定理),
∴△BCD是等边三角形;
∴∠CDB=60°.
(2)如图②,同(1)得出,∠BCD=60°,
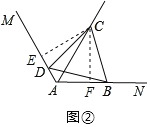
过点C作CE⊥AM于E,CF⊥AN于F,
∵AC是∠MAN的平分线,
∴CE=CF,
∵∠ABC+∠ADC=180°,∠ADC+∠CDE=180°,
∴∠CDE=∠ABC,
在△CDE和△CFB中,
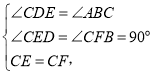
∴△CDE≌△CBF(AAS),
S四边形ABCD![]()
∴四边形ABCD的面积是个定值.

练习册系列答案
相关题目