Question

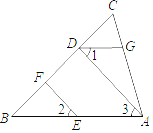
【题目】如图，在矩形ABCD中，AB=3，BC=2，点F是BC的中点，点E是边AB上一点，且BE=2，连结DE，EF，并以DE，EF为边作EFGD，连结BG，分别交EF和DC于点M，N，则 = ．

Answer 1

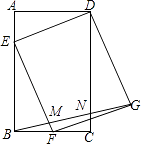
【答案】
【解析】解：∵矩形ABCD中，AB=3，BC=2，点F是BC的中点，

∴BF=1，AD=2，

又∵BE=2，

∴AE=BF=1，DE= =FG，

又∵∠A=∠EBF=90°，

∴△ADE≌△BEF，

∴∠ADE=∠BEF，DE=EF，

又∵∠ADE+∠AED=90°，

∴∠BEF+∠AED=90°，

∴∠DEF=90°，

∴四边形DEFG是正方形，

∴∠EFG=90°，DG=DE= ，

如图，过B作BH⊥EF于H，

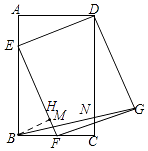
∵Rt△ABF中，EF= = ，

∴BH= = ，

∴Rt△BFH中，HF= = ，

∵BH∥FG，

∴△BHM∽△GFM，

∴ = = = ，

∴FM= ×FH= ，

∴EM=EF﹣FM= ﹣ = ，

∵EB∥DN，EM∥DG，

∴∠EBM=∠DNG，∠EMB=∠DGN，

∴△EBM∽△DNG，

∴ = = = ．

所以答案是： ．

【考点精析】本题主要考查了平行四边形的性质和矩形的性质的相关知识点，需要掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分；矩形的四个角都是直角，矩形的对角线相等才能正确解答此题．