题目内容
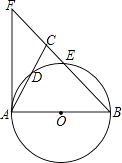
【题目】已知:△ABC是等腰直角三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰直角三角形PCQ,其中∠PCQ=90°,探究并解决下列问题:
(1)如图①,若点P在线段AB上,且AC=1+ ![]() ,PA=
,PA= ![]() ,则:
,则:
① 线段PB= , PC= ;
② 猜想:PA2 , PB2 , PQ2三者之间的数量关系为;
(2)如图②,若点P在AB的延长线上,在(1)中所猜想的结论仍然成立,请你利用图②给出证明过程;
(3)若动点P满足 ![]() =
= ![]() ,求
,求 ![]() 的值.(提示:请利用备用图进行探求)
的值.(提示:请利用备用图进行探求)
【答案】
(1)![]() ,2,AP2+BP2=PQ2
,2,AP2+BP2=PQ2
(2)解:如图②:过点C作CD⊥AB,垂足为D.
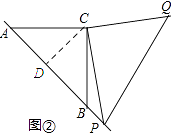
∵△ACB为等腰直角三角形,CD⊥AB,
∴CD=AD=DB.
∵AP2=(AD+PD)2=(DC+PD)2=CD2+2DCPD+PD2,
PB2=(DP﹣BD)2=(PD﹣DC)2=DC2﹣2DCPD+PD2,
∴AP2+BP2=2CD2+2PD2,
∵在Rt△PCD中,由勾股定理可知:PC2=DC2+PD2,
∴AP2+BP2=2PC2.
∵△CPQ为等腰直角三角形,
∴2PC2=PQ2.
∴AP2+BP2=PQ2.
(3)解:如图③:过点C作CD⊥AB,垂足为D.

①当点P位于点P1处时.
∵ ![]() ,
,
∴ ![]() .
.
∴ ![]() .
.
在Rt△CP1D中,由勾股定理得: ![]() =
= ![]() =
= ![]() DC,
DC,
在Rt△ACD中,由勾股定理得:AC= ![]() =
= ![]() =
= ![]() DC,
DC,
∴ ![]() .
.
②当点P位于点P2处时.
∵ ![]() =
= ![]() ,
,
∴ ![]() .
.
在Rt△CP2D中,由勾股定理得: ![]() =
= ![]() =
= ![]() ,
,
在Rt△ACD中,由勾股定理得:AC= ![]() =
= ![]() =
= ![]() DC,
DC,
∴ ![]() .
.
综上所述, ![]() 的比值为
的比值为 ![]() 或
或 ![]() .
.
【解析】(1)如图①:

①∵△ABC是等腰直直角三角形,AC=1+ ![]()
∴AB= ![]() =
= ![]() =
= ![]() +
+ ![]() ,
,
∵PA= ![]() ,
,
∴PB= ![]() ,
,
∵△ABC和△PCQ均为等腰直角三角形,
∴AC=BC,PC=CQ,∠ACP=∠BCQ,
∴△APC≌△BQC.
∴BQ=AP= ![]() ,∠CBQ=∠A=45°.
,∠CBQ=∠A=45°.
∴△PBQ为直角三角形.
∴PQ= ![]() .
.
∴PC= ![]() PQ=2.
PQ=2.
所以答案是: ![]() ,2;
,2;
②如图1.
∵△ACB为等腰直角三角形,CD⊥AB,
∴CD=AD=DB.
∵AP2=(AD﹣PD)2=(DC﹣PD)2=DC2﹣2DCPD+PD2,PB2=(DB+PD)2=(DC+DP)2=CD2+2DCPD+PD2
∴AP2+BP2=2CD2+2PD2,
∵在Rt△PCD中,由勾股定理可知:PC2=DC2+PD2,
∴AP2+BP2=2PC2.
∵△CPQ为等腰直角三角形,
∴2PC2=PQ2.
∴AP2+BP2=PQ2

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案