题目内容
【题目】如图，已知△ABC的三个顶点坐标如下表：
（1）将下表补充完整，并在直角坐标系中，画出△A′B′C′；
（x，y） | （2x，2y） |
A（2，1） | A′（4，2） |
B（4，3） | B′（ ） |
C（5，1） | C′（ ） |
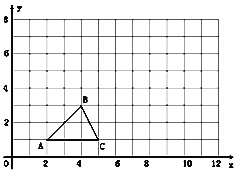
（2）观察两个三角形，可知△ABC∽△A′B′C′两个三角形的是以原点为位似中心的位似三角形，△ABC与△A′B′C′的位似比为 .
【答案】（1）B′( 8，6 )，C′（ 10，2 ）;（2）1：2
【解析】
(1)由表格所给倍数关系直接写出；(2)由图可知△ABC的一边AC长度为3，恰好为C与A点横坐标之差，故△A′B′C′的A′C′的长也可如此求解，则可得到两个三角形的相似比，即位似比.
解：(1)由表格所给数据可知B′点坐标为(8，6)，C’点坐标为(10，2)；
(2)由图可知△ABC的边AC长度为3，则△A′B′C′的A′C′长为10-4=6，则相似比为1:2，
故位似比为：1:2.
练习册系列答案
每课必练系列答案
巧学巧练系列答案
相关题目
