题目内容
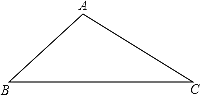
【题目】如图,![]() ,
,![]() ,
,![]() 为
为![]() 中点
中点
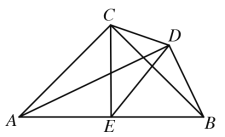
(1)若![]() ,求
,求![]() 的周长和面积.
的周长和面积.
(2)若![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)周长为![]() ,面积为
,面积为![]() ;(2)
;(2)![]()
【解析】
(1)根据直角三角形斜边上的中线等于斜边的一半可得CE=DE=![]() AB,即可求出周长,作底边CD上的高EH,利用勾股定理求出高,即可求面积;
AB,即可求出周长,作底边CD上的高EH,利用勾股定理求出高,即可求面积;
(2)设∠ECB=∠EBC=![]() ,则
,则![]() ,利用∠DEA=2∠DBE可推出∠CED=30°,作CE边上的高DM,利用30°所对的直角边是斜边的一半可求出高,再根据三角形面积公式求解.
,利用∠DEA=2∠DBE可推出∠CED=30°,作CE边上的高DM,利用30°所对的直角边是斜边的一半可求出高,再根据三角形面积公式求解.
(1)∵![]() ,
,![]() ,
,![]() 为
为![]() 中点
中点
∴CE=DE=![]() AB=3
AB=3
∴△CDE的周长=CE+DE+CD=3+3+2=8
如图,作EH⊥CD

∵CE=DE
∴CH=![]() CD=1
CD=1
![]()
∴S△CDE=![]()
(2)∵CE=DE=![]() AB,E为AB中点
AB,E为AB中点
∴CE=BE,DE=BE,
∴∠ECB=∠EBC,∠EBD=∠EDB
设∠ECB=∠EBC=![]() ,则∠CEA=2∠EBC=
,则∠CEA=2∠EBC=![]() ,
,
∴∠DEA=2∠EBD=![]()
∴∠CED=∠DEA-∠CEA=![]()
如图,过D点作DM⊥CE于点M,

由(1)可知在Rt△DEM中,DE=3,
∴DM=![]() DE=
DE=![]()
∴![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】如图,已知△ABC的三个顶点坐标如下表:
(1)将下表补充完整,并在直角坐标系中,画出△A′B′C′;
(x,y) | (2x,2y) |
A(2,1) | A′(4,2) |
B(4,3) | B′( ) |
C(5,1) | C′( ) |
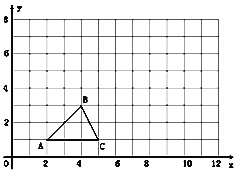
(2)观察两个三角形,可知△ABC∽△A′B′C′两个三角形的是以原点为位似中心的位似三角形,△ABC与△A′B′C′的位似比为 .