题目内容
【题目】如图所示,在平面直角坐标中,四边形OABC是梯形,且AB = OC = 4,CB∥OA,OA = 7,∠COA = 60°,点P为x轴上的—个动点,点P不与点0、点A重合.连结CP,过点P作PD交AB于点D,
(1)求点B的坐标;
(2)当点P运动什么位置时,使得∠CPD =∠OAB,且![]() ,求这时点P的坐标;
,求这时点P的坐标;
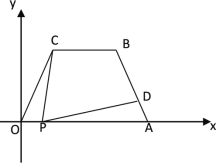
(3)当点P运动什么位置时,△OCP为等腰三角形,直接写出这时点P的坐标。
【答案】(1)![]() ; (2)
; (2) ![]() ;(3)
;(3)![]() .
.
【解析】
(1)过点B作![]() 于点Q,由等腰梯形可得∠BAO=∠COA=30°,再由30°角三角函数即可求解B点坐标;
于点Q,由等腰梯形可得∠BAO=∠COA=30°,再由30°角三角函数即可求解B点坐标;
(2)由三角形外角和可知∠CPA=∠OCP+∠COP,再由∠CPD =∠OAB可得∠OCP=∠APD,结合∠DAP=∠COP=60°可证明![]() ∽
∽![]() ,利用相似比可求解P点坐标;
,利用相似比可求解P点坐标;
(3)分点P在O点右侧和左侧两种情况分别讨论.
解:(1)过点B作![]() 于点Q,
于点Q,
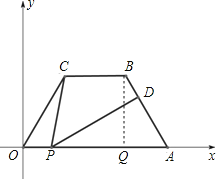
则![]() ,在
,在![]() 中,
中,
![]() ,
,![]() ,则
,则![]() ,
,
故B点坐标为![]() ;
;
(2) ![]()
![]()
![]()
![]()
![]()
![]() ∽
∽![]()
![]()
![]()
![]()
即![]()
![]()
![]()
(3)当点P在O点右侧时,△OCP为等边三角形,OP=4,则P(4,0);当点P在O点左侧时,OP=OC=4,则P(-4,0).

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
【题目】如图,已知△ABC的三个顶点坐标如下表:
(1)将下表补充完整,并在直角坐标系中,画出△A′B′C′;
(x,y) | (2x,2y) |
A(2,1) | A′(4,2) |
B(4,3) | B′( ) |
C(5,1) | C′( ) |
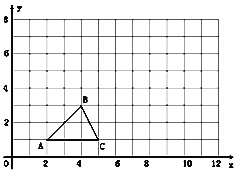
(2)观察两个三角形,可知△ABC∽△A′B′C′两个三角形的是以原点为位似中心的位似三角形,△ABC与△A′B′C′的位似比为 .