题目内容
【题目】(本题满分7分)已知关于x的方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
(1)求k的取值范围;
(2)是否存在实数k,使此方程的两个实数根的倒数和等于0?若存在,求出k的值;若不存在,说明理由.
【答案】(1)![]() ,且
,且![]() ;(2)不存在,理由见试题解析.
;(2)不存在,理由见试题解析.
【解析】
试题(1)根据方程有两个不相等的实数根可知△=![]() ,求得k的取值范围;
,求得k的取值范围;
(2)可假设存在实数k,使得方程的两个实数根![]() ,
,![]() 的倒数和为0,列出方程即可求得k的值,然后把求得的k值代入原式中看看与已知是否矛盾,如果矛盾则不存在,如果不矛盾则存在.
的倒数和为0,列出方程即可求得k的值,然后把求得的k值代入原式中看看与已知是否矛盾,如果矛盾则不存在,如果不矛盾则存在.
试题解析:(1)∵方程有两个不相等的实数根,
∴△=![]() ,且
,且![]() ,解得
,解得![]() ,且
,且![]() ,即k的取值范围是
,即k的取值范围是![]() ,且
,且![]() ;
;
(2)假设存在实数k,使得方程的两个实数根![]() ,
,![]() 的倒数和为0,则
的倒数和为0,则![]() ,
,![]() 不为0,且
不为0,且![]() ,即
,即![]() ,且
,且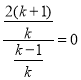 ,解得
,解得![]() ,而
,而![]() 与方程有两个不相等实根的条件
与方程有两个不相等实根的条件![]() ,且
,且![]() 矛盾,故使方程的两个实数根的倒数和为0的实数k不存在.
矛盾,故使方程的两个实数根的倒数和为0的实数k不存在.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目