题目内容
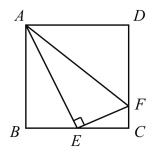
【题目】如图,在正方形 ABCD 中,E是BC的中点,F是CD上一点,AE⊥EF.有下列结论:
①∠BAE=30°;
②射线FE是∠AFC的角平分线;
③CF=![]() CD;
CD;
④AF=AB+CF.
其中正确结论的个数为( )
A.1 个B.2 个C.3 个D.4 个
【答案】B
【解析】
根据点E为BC中点和正方形的性质,得出∠BAE的正切值,从而判断①,再证明△ABE∽△ECF,利用有两边对应成比例且夹角相等三角形相似即可证得△ABE∽△AEF,可判断②③,过点E作AF的垂线于点G,再证明△ABE≌△AGE,△ECF≌△EGF,即可证明④.
解:∵E是BC的中点,
∴tan∠BAE=![]() ,
,
∴∠BAE![]() 30°,故①错误;
30°,故①错误;
∵四边形ABCD是正方形,
∴∠B=∠C=90°,AB=BC=CD,
∵AE⊥EF,
∴∠AEF=∠B=90°,
∴∠BAE+∠AEB=90°,∠AEB+FEC=90°,
∴∠BAE=∠CEF,
在△BAE和△CEF中,
![]() ,
,
∴△BAE∽△CEF,
∴![]() ,
,
∴BE=CE=2CF,
∵BE=CF=![]() BC=
BC=![]() CD,
CD,
即2CF=![]() CD,
CD,
∴CF=![]() CD,
CD,
故③错误;
设CF=a,则BE=CE=2a,AB=CD=AD=4a,DF=3a,
∴AE=![]() a,EF=
a,EF=![]() a,AF=5a,
a,AF=5a,
∴![]() ,
,![]() ,
,
∴![]() ,
,
又∵∠B=∠AEF,
∴△ABE∽△AEF,
∴∠AEB=∠AFE,∠BAE=∠EAG,
又∵∠AEB=∠EFC,
∴∠AFE=∠EFC,
∴射线FE是∠AFC的角平分线,故②正确;
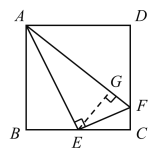
过点E作AF的垂线于点G,
在△ABE和△AGE中,
 ,
,
∴△ABE≌△AGE(AAS),
∴AG=AB,GE=BE=CE,
在Rt△EFG和Rt△EFC中,
![]() ,
,
Rt△EFG≌Rt△EFC(HL),
∴GF=CF,
∴AB+CF=AG+GF=AF,故④正确.
故选B.

【题目】为了了解学生对“预防新型冠状病毒”知识的掌握情况,学校组织了一次线上知识培训,培训结束后进行测试,在全校2000名学生中,分别抽取了男生,女生各15份成绩,整理分析过程如下,请补充完整.
(收集数据)
15名男生测试成绩统计如下:(满分100分)78,90,99,93,92,95,94,100,90,85,86,95,75,88,90
15名女生测试成绩统计如下:(满分100分)77,82,83,86,90,90,92,91,93,92,92,92,92,98,100
(整理、描述数据)
70.5~75.5 | 75.5~80.5 | 80.5~85.5 | 85.5~90.5 | 90.5~95.5 | 95.5~100.5 | |
男生 | 1 | 1 | 1 | 5 | 5 | 2 |
女生 | 0 | 1 | 2 | 3 | 7 | 2 |
(分析数据)
(1)两组样本数据的平均数、众数、中位数、方差如下表所示:
性别 | 平均数 | 众数 | 中位数 | 方差 |
男生 | 90 | 90 | 90 | 44.9 |
女生 | 90 |
|
| 32.8 |
在表中:![]() ________.
________.![]() ________;
________;
(2)若规定得分在80分以上(不含80分)为合格,请估计全校学生中“预防新型冠状病毒”知识测试合格的学生有多少人?
(3)通过数据分析得到的结论,你认为男生和女生中谁的成绩比较好?请说明理由.