Question

【题目】如图，抛物线与轴相交于、两点，与轴相交于点，且点与点的坐标分别为，，点是抛物线的顶点．

（1）求二次函数的关系式．

（2）点为线段上一个动点，过点作轴于点．若，的面积为．

①求与的函数关系式，写出自变量的取值范围．

②当取得最值时，求点的坐标．

（3）在上是否存在点，使为直角三角形？如果存在，请直接写出点的坐标；如果不存在，请说明理由．

Answer 1

【答案】（1）；（2）①，；②P（，3）；

（3）或

【解析】

（1）将点B、C的坐标代入即可；

（2）①求出顶点坐标，直线MB的解析式等，由PD⊥x轴且OD=m知P（m，-2m+6），即可用含m的代数式表示出S；

②在和①的情况下，将S和m的关系式化为顶点式，由二次函数的图象和性质即可写出点P的坐标；

（3）分情况讨论，当∠CPD=90°时，推出PD=CO=3，则点P的纵坐标为3，即可求出点P的坐标；当∠PCD=90°时，证∠PDC=∠OCD，由锐角三角函数可求出m的值，即可写出点P的坐标；当∠PDC=90°时，不存在点P．

解：（1）将，代入，

得，

解得，

∴二次函数的解析式为；

（2）①∵

∴顶点M（1，4），

将直线BM的解析式设为，

将点，M（1，4）代入，

可得，

解得，

∴直线BM的解析式为，

如图∵PD⊥x轴且OD=m，

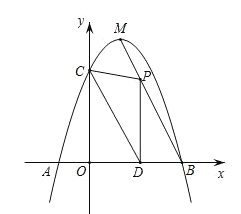
∴P（m，-2m+6），

∴，

即，

∵点为线段上一个动点且，M（1，4），

∴；

②，

∴当时，S取最大值，

∴P（，3）；

（3）存在，理由如下：

如图，当∠CPD=90°时，

,

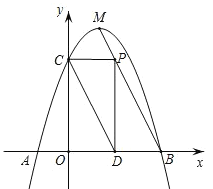
∴四边形CODP为矩形，

∵PD=CO=3,

将代入直线，

得，

∴P；

如图，当∠PCD=90°时，

∵OC=3，OD=m，

，

,

,

,

,

，

解得（舍去），，

∴；

当∠PDC=90°时，

∵PD⊥x轴，

∴不存在点P；

综上所述，点P的坐标为或．