题目内容
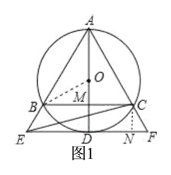
【题目】如图,⊙O是△ABC的外接圆,AD是⊙O的直径,AD与BC相交于点M,且BM=MC,过点D作BC的平行线,分别与AB、AC的延长线相交于点E、F.
(1)求证:EF与⊙O相切;
(2)若BC=2![]() ,MD=
,MD=![]() ,求CE的长.
,求CE的长.

【答案】(1)见解析;(2)![]()
【解析】试题分析:
(1)由AD是⊙O的直径,BM=MC可得AD⊥BC,结合EF∥BC可得AD⊥EF,从而根据“切线的判定定理”可得EF与⊙O相切;
(2)如图1,连接OB,过点C作CN⊥EF于点N.先证△OBM是Rt△,由勾股定理建立方程解此OB的长,因此可得AD的长和AM的长;证△ABC∽△AEF,从而可解得EF的长;在Rt△AMC中,计算出tan∠AMC的值,从而可得∠MAC=30°,由此可得∠NCF=30°,结合CN=MD可在Rt△NCF中解得得NF的长,即可由EN=EF-NF得到EN的长,这样在Rt△ECN中即可由勾股定理解得CE的长了.
试题解析:
(1)∵AD是⊙O的直径,AD与BC相交于点M,且BM=MC,
∴AD⊥BC,
∵EF∥BC,
∴AD⊥EF,
∴EF与⊙O相切;
(2)连接OB,
在△OBM中,BM2+OM2=OB,即(![]() )+(OB﹣
)+(OB﹣![]() )=OB2,OB=2
)=OB2,OB=2![]()
∴OM=MD=![]() ,
,
∵BC∥EF,
∴△ABC∽△AEF
∴![]() ,
,
∴EF=![]() =
=![]() =
=![]() ,
,
∵tan∠CAM=![]() ,
,
∴∠CAM=30°,
作CN⊥EF,
∵AD⊥EF,
∴CN∥AD,
∴∠FCN=∠CAM=30°,
∵BC∥EF,
∴四边形MDNC是矩形,
∴CN=MD=![]() ,
,
∴NF=CNtan30°=![]() ×
×![]() =
=![]() ,
,
∴EN=EF﹣NF=![]() ﹣
﹣![]() =
=![]() ,
,
∴EC=![]() =
=![]() .
.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目





