Question

设a、b、c均不为0，且a+b+c=1998，

1

a

+

1

b

+

1

c

=

1

1998

，求证：a、b、c中至少有一个等于1998．

Answer 1

证明：
∵a+b+c=1998，

1

a

+

1

b

+

1

c

=

1

1998

∴

1

a

+

1

b

+

1

c

=

1

a+b+c

?

ab+bc+ac

abc

=

1

a+b+c

?（ab+bc+ac）（a+b+c）=abc?（a+b）（ab+bc+ac）+（ab+bc+ac）c=abc?（a+b）（ab+bc+ac）+abc+c（bc+ac）=abc?（a+b）（ab+bc+ac）+c²（a+b）=0?（a+b）（ab+bc+ac+c²）=0?（a+b）[b（a+c）+c（a+c）]=0?（a+b）（a+b）（a+c）=0
∴a+b，b+c，c+a中必有一个为0
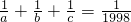∴a、b、c中至少有一个等于1998