题目内容
设a、b、c均不为0,且a+b+c=1998,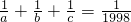 ,求证:a、b、c中至少有一个等于1998.
,求证:a、b、c中至少有一个等于1998.
证明:
∵a+b+c=1998,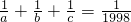
∴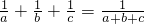 ?
?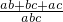 =
=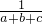 ?(ab+bc+ac)(a+b+c)=abc?(a+b)(ab+bc+ac)+(ab+bc+ac)c=abc?(a+b)(ab+bc+ac)+abc+c(bc+ac)=abc?(a+b)(ab+bc+ac)+c2(a+b)=0?(a+b)(ab+bc+ac+c2)=0?(a+b)[b(a+c)+c(a+c)]=0?(a+b)(a+b)(a+c)=0
?(ab+bc+ac)(a+b+c)=abc?(a+b)(ab+bc+ac)+(ab+bc+ac)c=abc?(a+b)(ab+bc+ac)+abc+c(bc+ac)=abc?(a+b)(ab+bc+ac)+c2(a+b)=0?(a+b)(ab+bc+ac+c2)=0?(a+b)[b(a+c)+c(a+c)]=0?(a+b)(a+b)(a+c)=0
∴a+b,b+c,c+a中必有一个为0
∴a、b、c中至少有一个等于1998
分析:要想证明a、b、c中至少有一个等于1998,根据a+b+c=1998,只需证明a+b=0或a+c=0或b+c=0即可,首先将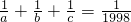 中的1998用a+b+c表示,即
中的1998用a+b+c表示,即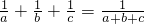 ,去分母、分解因式,转化为(a+b)(b+c)(c+a)=0的形式.
,去分母、分解因式,转化为(a+b)(b+c)(c+a)=0的形式.
点评:本题考查分式的混合运算.解决本题的关键是将证明a、b、c中至少有一个等于1998,转化为证明a+b=0或a+c=0或b+c=0.
∵a+b+c=1998,
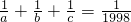
∴
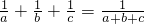 ?
?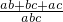 =
=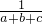 ?(ab+bc+ac)(a+b+c)=abc?(a+b)(ab+bc+ac)+(ab+bc+ac)c=abc?(a+b)(ab+bc+ac)+abc+c(bc+ac)=abc?(a+b)(ab+bc+ac)+c2(a+b)=0?(a+b)(ab+bc+ac+c2)=0?(a+b)[b(a+c)+c(a+c)]=0?(a+b)(a+b)(a+c)=0
?(ab+bc+ac)(a+b+c)=abc?(a+b)(ab+bc+ac)+(ab+bc+ac)c=abc?(a+b)(ab+bc+ac)+abc+c(bc+ac)=abc?(a+b)(ab+bc+ac)+c2(a+b)=0?(a+b)(ab+bc+ac+c2)=0?(a+b)[b(a+c)+c(a+c)]=0?(a+b)(a+b)(a+c)=0∴a+b,b+c,c+a中必有一个为0
∴a、b、c中至少有一个等于1998
分析:要想证明a、b、c中至少有一个等于1998,根据a+b+c=1998,只需证明a+b=0或a+c=0或b+c=0即可,首先将
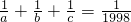 中的1998用a+b+c表示,即
中的1998用a+b+c表示,即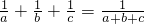 ,去分母、分解因式,转化为(a+b)(b+c)(c+a)=0的形式.
,去分母、分解因式,转化为(a+b)(b+c)(c+a)=0的形式.点评:本题考查分式的混合运算.解决本题的关键是将证明a、b、c中至少有一个等于1998,转化为证明a+b=0或a+c=0或b+c=0.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目