题目内容
如图,直角梯形ABCD的顶点A、B、C的坐标分别为( ,0)、(2,0)和(2,3),AB∥CD,∠C=90°,CD=CB。
,0)、(2,0)和(2,3),AB∥CD,∠C=90°,CD=CB。
(1)求点D的坐标;
(2)抛物线y=ax2+bx+c过原点O与点(7,1),且对称轴为过点(4,3)与y轴平行的直线,求抛物线的函数关系式;
(3)在(2)中的抛物线上是否存在一点P,使得PA+PB+PC+PD最小?若存在,求出点P的坐标;若不存在,请说明理由。
 ,0)、(2,0)和(2,3),AB∥CD,∠C=90°,CD=CB。
,0)、(2,0)和(2,3),AB∥CD,∠C=90°,CD=CB。(1)求点D的坐标;
(2)抛物线y=ax2+bx+c过原点O与点(7,1),且对称轴为过点(4,3)与y轴平行的直线,求抛物线的函数关系式;
(3)在(2)中的抛物线上是否存在一点P,使得PA+PB+PC+PD最小?若存在,求出点P的坐标;若不存在,请说明理由。

解:(1)D(-1,3);
(2)设抛物线解析式为y=ax2+bx+c
由题意得: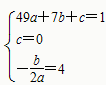 ,∴
,∴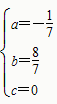
∴ y=-x2+x;
(3)显然AC、BD的交点Q满足QA+QB+QC+QD最小,
直线AC的解析式为y=2x-1,
直线BD的解析式为y=-x+2,
∴ Q(1,1)
当x=1时,y=-x2+x=1,
∴ 点Q在此抛物线上,
∴ 存在点P(1,1)使得PA+PB+PC+PD最小。
(2)设抛物线解析式为y=ax2+bx+c
由题意得:
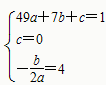 ,∴
,∴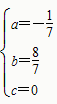
∴ y=-x2+x;
(3)显然AC、BD的交点Q满足QA+QB+QC+QD最小,
直线AC的解析式为y=2x-1,
直线BD的解析式为y=-x+2,
∴ Q(1,1)
当x=1时,y=-x2+x=1,
∴ 点Q在此抛物线上,
∴ 存在点P(1,1)使得PA+PB+PC+PD最小。

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是AB边上一点,AE=BC,DE⊥EC,取DC的中点F,连接AF、BF.
如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是AB边上一点,AE=BC,DE⊥EC,取DC的中点F,连接AF、BF. ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.
ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF. 如图,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2.
如图,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2. (2013•深圳二模)如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD为边在直角梯形ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.
(2013•深圳二模)如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD为边在直角梯形ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF. 已知:如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,以AB为直径的⊙O切DC边于E点,AD=3cm,BC=5cm.求⊙O的面积.
已知:如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,以AB为直径的⊙O切DC边于E点,AD=3cm,BC=5cm.求⊙O的面积.