题目内容
 (2013•深圳二模)如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD为边在直角梯形ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.
(2013•深圳二模)如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD为边在直角梯形ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.(1)求证:EB=EF;
(2)若EF=6,求梯形ABCD的面积.
分析:(1)由三角形ADF为等边三角形,利用等边三角形的性质得到AF=AD,∠FAD=60°,再由∠FAD+∠EAD求出∠EAF的度数,由∠DAB-∠EAD求出∠BAE的度数,得到∠FAE=∠BAE,再由AB=AD,等量代换得到AF=AB,再由AE为公共边,利用SAS可得出三角形AEF与三角形AEB全等,由全等三角形的对应边相等可得出EF=EB,得证;
(2)由FD=FA,DE=AE,以及公共边FE,利用SSS可得出三角形DEF与三角形AEF全等,由全等三角形的性质及等边三角形的性质得到∠DFE=∠AFE=30°,求出∠DEF为75°,在由∠FAE+∠EAD求出∠FAE为75°,可得出∠FAE=∠FEA,利用等角对等边得到FE=AF,可得出等边三角形AFD三边长为6,过C作CM垂直于AB,可得出CM=6,由∠ABC为60°,在直角三角形BCM中,利用锐角三角函数定义及特殊角的三角函数值求出BM的长,由AB-BM求出AM的长,即为DC的长,利用利用梯形的面积公式即可求出梯形ABCD的面积.
(2)由FD=FA,DE=AE,以及公共边FE,利用SSS可得出三角形DEF与三角形AEF全等,由全等三角形的性质及等边三角形的性质得到∠DFE=∠AFE=30°,求出∠DEF为75°,在由∠FAE+∠EAD求出∠FAE为75°,可得出∠FAE=∠FEA,利用等角对等边得到FE=AF,可得出等边三角形AFD三边长为6,过C作CM垂直于AB,可得出CM=6,由∠ABC为60°,在直角三角形BCM中,利用锐角三角函数定义及特殊角的三角函数值求出BM的长,由AB-BM求出AM的长,即为DC的长,利用利用梯形的面积公式即可求出梯形ABCD的面积.
解答: 解:(1)证明:∵△ADF为等边三角形,
解:(1)证明:∵△ADF为等边三角形,
∴AF=AD,∠FAD=60°,
∵∠DAB=90°,∠EAD=15°,
∴∠FAE=∠FAD+∠EAD=75°,∠BAE=∠DAB-∠EAD=75°,
∴∠FAE=∠BAE,
又∵AD=AB,
∴AB=AF,
在△FAE和△BAE中,
,
∴△FAE≌△BAE(SAS),
∴EF=EB;
(2)在△FAE和△FDE中,
,
∴△FAE≌△FDE(SSS),
∴∠DFE=∠AFE=
×60°=30°,∠DEF=∠AEF=
×150°=75°,
又∵∠FAE=60°+15°=75°,
∴∠AEF=∠FAE,
又∵EF=6,
∴AF=EF=6,AB=AD=AF=6,
过C作CM⊥AB于M,可得CM=AD=6,
∵tan∠ABC=
,∠ABC=60°,
∴BM=
=
=2
,
∴CD=AM=AB-BM=6-2
,
∴S梯形ABCD=
×[(6-2
)+6]×6=36-6
.
 解:(1)证明:∵△ADF为等边三角形,
解:(1)证明:∵△ADF为等边三角形,∴AF=AD,∠FAD=60°,
∵∠DAB=90°,∠EAD=15°,
∴∠FAE=∠FAD+∠EAD=75°,∠BAE=∠DAB-∠EAD=75°,
∴∠FAE=∠BAE,
又∵AD=AB,
∴AB=AF,
在△FAE和△BAE中,
|
∴△FAE≌△BAE(SAS),
∴EF=EB;
(2)在△FAE和△FDE中,
|
∴△FAE≌△FDE(SSS),
∴∠DFE=∠AFE=
| 1 |
| 2 |
| 1 |
| 2 |
又∵∠FAE=60°+15°=75°,
∴∠AEF=∠FAE,
又∵EF=6,
∴AF=EF=6,AB=AD=AF=6,
过C作CM⊥AB于M,可得CM=AD=6,
∵tan∠ABC=
| CM |
| BM |
∴BM=
| CM |
| tan60° |
| 6 | ||
|
| 3 |
∴CD=AM=AB-BM=6-2
| 3 |
∴S梯形ABCD=
| 1 |
| 2 |
| 3 |
| 3 |
点评:此题考查了直角梯形,全等三角形的判定与性质,等边三角形的性质,锐角三角函数定义,以及梯形的面积公式,是一道综合性较强的试题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
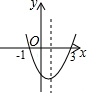 (2013•深圳二模)如图,为二次函数y=ax2+bx+c的图象,给出的下列6个结论:
(2013•深圳二模)如图,为二次函数y=ax2+bx+c的图象,给出的下列6个结论: