题目内容
 如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是AB边上一点,AE=BC,DE⊥EC,取DC的中点F,连接AF、BF.
如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是AB边上一点,AE=BC,DE⊥EC,取DC的中点F,连接AF、BF.(1)求证:AD=BE;
(2)试判断△ABF的形状,并说明理由.
分析:(1)根据平行线的性质和三角形的内角和定理推出∠BEC=∠ADE,根据AAS证出△EAD≌△EBC即可;
(2)延长AF交BC的延长线于M,证△ADF≌△MFC,推出AF=FM,根据等腰三角形性质推出AF⊥BF,根据直角三角形斜边上中线性质推出AF=BF即可.
(2)延长AF交BC的延长线于M,证△ADF≌△MFC,推出AF=FM,根据等腰三角形性质推出AF⊥BF,根据直角三角形斜边上中线性质推出AF=BF即可.
解答:(1)证明:∵AD∥BC,
∴∠BAD+∠ABC=180°,
∵∠ABC=90°,
∴∠BAD=∠ABC=90°,
∵DE⊥EC,
∴∠AED+∠BEC=90°
∵∠AED+∠ADE=90°,
∴∠BEC=∠ADE,
∵∠DAE=∠EBC,AE=BC,
∴△EAD≌△EBC,
∴AD=BE.
(2)答:△ABF是等腰直角三角形.
理由是:延长AF交BC的延长线于M,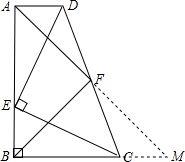
∵AD∥BM,
∴∠DAF=∠M,
∵∠AFD=∠CFM,DF=FC,
∴△ADF≌△MFC,
∴AD=CM,
∵AD=BE,
∴BE=CM,
∵AE=BC,
∴AB=BM,
∴△ABM是等腰直角三角形,
∵△ADF≌△MCF,
∴AF=FM,
∴∠ABC=90°,
∴BF⊥AM,BF=
AM=AF,
∴△AFB是等腰直角三角形.
∴∠BAD+∠ABC=180°,
∵∠ABC=90°,
∴∠BAD=∠ABC=90°,
∵DE⊥EC,
∴∠AED+∠BEC=90°
∵∠AED+∠ADE=90°,
∴∠BEC=∠ADE,
∵∠DAE=∠EBC,AE=BC,
∴△EAD≌△EBC,
∴AD=BE.
(2)答:△ABF是等腰直角三角形.
理由是:延长AF交BC的延长线于M,

∵AD∥BM,
∴∠DAF=∠M,
∵∠AFD=∠CFM,DF=FC,
∴△ADF≌△MFC,
∴AD=CM,
∵AD=BE,
∴BE=CM,
∵AE=BC,
∴AB=BM,
∴△ABM是等腰直角三角形,
∵△ADF≌△MCF,
∴AF=FM,
∴∠ABC=90°,
∴BF⊥AM,BF=
| 1 |
| 2 |
∴△AFB是等腰直角三角形.
点评:本题主要考查对直角梯形,直角三角形斜边上的中线,等腰直角三角形,等腰三角形的性质,全等三角形的性质和判定,平行线的性质等知识点的理解和掌握,综合运用这些性质进行推理是解此题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.
ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF. 如图,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2.
如图,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2. (2013•深圳二模)如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD为边在直角梯形ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.
(2013•深圳二模)如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD为边在直角梯形ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF. 已知:如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,以AB为直径的⊙O切DC边于E点,AD=3cm,BC=5cm.求⊙O的面积.
已知:如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,以AB为直径的⊙O切DC边于E点,AD=3cm,BC=5cm.求⊙O的面积.